Cho khối lăng trụ ABC. A'B'C' có thể tích bằng 2018. Gọi M là trung điểm AA' ; N, P lần lượt là các điểm nằm trên các cạnh BB', CC' sao cho BN=2B'N, CP=3C'P. Tính thể tích khối đa diện ABC. MNP.
A. 32288 27
B. 40360 27
C. 4036 3
D. 23207 18
Cho khối lăng trụ ABC. A'B'C'. Gọi E là trọng tâm tam giác A'B'C' và F là trung điểm BC. Tính tỉ số thể tích giữa khối B'. EAF và khối lăng trụ ABC. A'B'C'.
A. 1 4
B. 1 8
C. 1 5
D. 1 6
Cho lăng trụ A B C A ' B ' C ' , trên cạnh AA';BB' lấy các điểm M, N sao cho A A ' = 3 A ' M ; B B ' = 3 B ' N . A A ' = 3 A ' M ; B B ' = 3 B ' N Mặt phẳng chia khối lăng trụ đã cho thành hai phần. Gọi V 1 là thể tích khối chóp C'A'B'NM , V 2 là thể tích khối đa diện ABC.MNC'. Tính tỉ số V 1 V 2
A. 2 9
B. 3 4
C. 2 7
D. 5 7
Đáp án C.
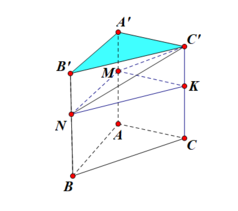
V A B C . M N K = S A B C . C K = 2 3 S A B C . A ' A
V
C
'
M
K
=
1
3
C
'
K
.
S
=
1
9
C
'
C
'
S
A
B
C
=
1
9
A
'
.
A
.
S
A
B
C
⇒
V
2
=
V
A
B
C
.
M
N
K
+
V
C
'
.
M
N
K
=
2
3
S
A
B
C
.
A
A
'
+
1
9
A
'
A
.
S
A
B
C
=
7
9
A
'
A
.
S
A
B
C
V
M
N
K
A
'
B
'
C
'
=
S
M
N
K
.
C
'
K
=
1
3
S
A
B
C
.
A
'
A
⇒ V 1 = V M N K A ' B ' C ' - V C ' M N K = 1 3 S A B C . A ' A - 1 9 A ' A S A B C = 2 9 A ' A S A B C
Vậy : V 1 V 2 = 2 9 A ' A S A B C 7 9 A ' A S A B C = 2 7 .
Xét khối lăng trụ tam giác ABC. A'B'C'. Mặt phẳng đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ thành hai phần có tỉ số thể tích bằng:
A. 2 3
B. 1 2
C. 1
D. 1 3
Chọn B
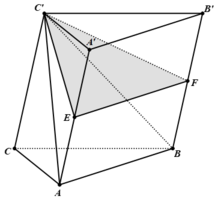
Gọi E, F lần lượt là các trung điểm của AA' và BB' khi đó ta có:
Vậy mặt phẳng (C'EF) chia khối lăng trụ thành hai phần có tỉ số thể tích bằng 1 2 .
Cho hinh lăng trụ A'B'C' có đáy ABC là tam giác đều cạnh a, hình chiếu của A' trên (ABC) là trung điểm đoạn thẳng AB. Biết AA’ = 2a. Thể tích của khối lăng trụ A'B'C'ABC là
Do \(AA'\text{/ / }CC'\Rightarrow AA'\) tạo với (ABC) một góc \(45^o\)
Mà \(A'H\text{⊥}\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa \(AA'\) và ( ABC)
\(\Rightarrow\widehat{A'AH=45^o\Rightarrow}\Delta A'AH\) vuông cân tại H
\(\Rightarrow A'H=AH=\dfrac{AB}{2}=\dfrac{a}{2}\)
\(^SABC=\dfrac{a^2\sqrt{3}}{4}=V=^SABC.^{A'H}=\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3.\sqrt{3}}{8}\)
Cho khối lăng trụ đứng, mặt phẳng (P) đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ ABC. A'B'C' thành hai khối đa diện có tỷ số thể tích bằng k với k ≤ 1. Tìm k.
A. 1 3
B. 2 3
C. 1
D. 1 2
Chọn D
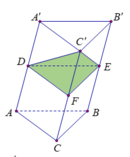
Gọi D, E, F lần lượt là trung điểm của AA', BB', CC' và h là độ dài chiều cao của khối lăng trụ ABC. A'B'C'. Khi đó ta có:
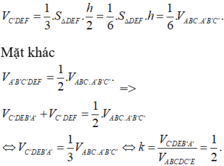
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 2018. Gọi M là trung điểm AA’; N, P lần lượt là các điểm nằm trên các cạnh BB’, CC’ sao cho B N = 2 B ' N , C P = 3 C ' P . Tính thể tích khối đa diện ABCMNP
A. 4036 3
B. 32288 27
C. 40360 27
D. 23207 18
Cho khối lăng trụ ABC A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, C. Cạnh bên AA' tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC A'B'C' là
A. a 3 3
B. a 3 3 2
C. a 3 3 6
D. a 3 3 4
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a√2 . Gọi I là trung điểm B'C góc giữa AI và đáy bằng 60. Tính thể tích V của khối lăng trụ ABC. A'B'C' .
Cho hình lăng trụ đều A B C . A ' B ' C ' có tất cả các cạnh bằng 1. Gọi E, F lần lượt là trung điểm của AA’ và BB’; đường thẳng CE cắt đường thẳng C’A’ tại E’, đường thẳng CF cắt đường thẳng C’B’ tại F’. Thể tích khối đa diện E F A ’ B ’ E ’ F ’ bằng
A. 3 12
B. 3 2
C. 3 3
D. 3 6