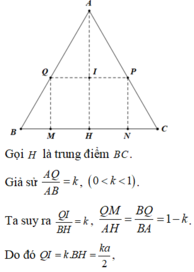
cho tam giác ABC. Dựng ngoài ΔABC hình chữ nhật BCDG. Dựng DE⊥AB và GF⊥AC; DE và GF cắt nhau tại L. Vẽ \(\overrightarrow{AK}\) =\(\overrightarrow{CD}\). CM rằng AL⊥BC

Những câu hỏi liên quan
Cho tam giác đều ABC có cạnh 8 cm. Dựng hình chữ nhật MNPQ với cạnh MN nằm trên cạnh BC và hai đỉnh P, Q lần lượt nằm trên cạnh AC, AB của tam giác. Tính BM sao cho hình chữ nhật MNPQ có diện tích lớn nhất. A. BM 2cm B. BM8
3
cm C. BM 4cm D. BM4
2
cm
Đọc tiếp
Cho tam giác đều ABC có cạnh 8 cm. Dựng hình chữ nhật MNPQ với cạnh MN nằm trên cạnh BC và hai đỉnh P, Q lần lượt nằm trên cạnh AC, AB của tam giác. Tính BM sao cho hình chữ nhật MNPQ có diện tích lớn nhất.
A. BM = 2cm
B. BM=8 3 cm
C. BM = 4cm
D. BM=4 2 cm
Cho tam giác đều ABC có cạnh 8 cm. Dựng hình chữ nhật MNPQ với cạnh MN nằm trên cạnh BC và hai đỉnh P, Q lần lượt nằm trên cạnh AC, AB của tam giác. Tính BM sao cho hình chữ nhật MNPQ có diện tích lớn nhất
A. BM=2cm
B. BM=4cm
C. BM=6cm
D. BM=8cm
Lấy 2 cạnh AB và AC của tam giác ABC, dựng ra phía ngoài của góc A 2 tam giác đều là tam giác ABD và ACE. Lấy AD, AE là 2 cạnh dựng hình bình hành ADEF. C/m tam giác FBC đều
Cho tam giác ABC nhọn ( AB < AC). Ngoài tam giác ABC dựng các hình vuông BCDE, ACFG, ABKH và các hình bình hành BEQK, CDPF. Chứng minh tam giác APQ vuông cân.
Các bạn vẽ hình và làm giúp mình nha!!!
Cho một tam giác đều ABC cạnh A. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định giá trị lớn nhất của diện tích hình chữ nhật đó. B. 0
Đọc tiếp
Cho một tam giác đều ABC cạnh A. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định giá trị lớn nhất của diện tích hình chữ nhật đó.
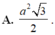
B. 0
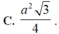
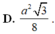
cho hình chữ nhật ABCD. Về phía ngoài hình chữ nhật dựng tam giác BCE vuông tại C có góc CBE= 45 độ và dựng tam giác ABF vuông tại F có À=6cm, BF=8cm. Biết BE = căn 18. TÍnh chu vi ngũ giác ADEBF
1) Cho tam giác ABC phân giác AD. Qua D dựng đường thẳng song song với AB đường thẳng này cắt AC tại E. Qua E dựng đường thẳng song song với BC đường thẳng này cắt AB tại F. a) chứng minh AEAF, b) Xác định hình dạng của tam giác ABC trong trường hợp E là trung điểm AC.2) Cho hình bình hành ABCD. Từ B kẻ BH vuông góc với AC. Gọi M,N,P,Q lần lượt là trung điểm của AH,AB,NB,BC. a) MP1/2 NC. b) chứng minh BM vuông góc với NQ.3) cho tam giác ABC, các đường thẳng AP,AQ theo thứ tự vuông góc với phân g...
Đọc tiếp
1) Cho tam giác ABC phân giác AD. Qua D dựng đường thẳng song song với AB đường thẳng này cắt AC tại E. Qua E dựng đường thẳng song song với BC đường thẳng này cắt AB tại F. a) chứng minh AE=AF, b) Xác định hình dạng của tam giác ABC trong trường hợp E là trung điểm AC.
2) Cho hình bình hành ABCD. Từ B kẻ BH vuông góc với AC. Gọi M,N,P,Q lần lượt là trung điểm của AH,AB,NB,BC. a) MP=1/2 NC. b) chứng minh BM vuông góc với NQ.
3) cho tam giác ABC, các đường thẳng AP,AQ theo thứ tự vuông góc với phân giác trong và phân giác ngoài góc B. Các đoạn thẳng AR, AS vuông góc phân giác trong và phân giác ngoài góc C. a) chứng minh APBQ, ÁC là hình chữ nhật, b) Q,R,P,S thẳng hàng, c) QS=1/2 (AB+BC+AC)
Cho tam giác ABC. Lấy cạnh AB, AC làm đáy, dựng ra ngoài các tam giác cân đồng dạng ABC', CAB'. lấy cạnh BC làm đáy, dựng vào trong tam giác cân BCA' đồng dạng với hai tam giác cân kia. Chứng minh rằng AB'A'C' là một hình bình hành
Gọi D, E và F theo thứ tự là trung điểm các cạnh BC, CA và AB của tam giác ABC. Ta có :
\(\overrightarrow{AB'}=\overrightarrow{AE}+\overrightarrow{EB'}=\frac{1}{2}\overrightarrow{c}+\overrightarrow{EB'}\)
\(\overrightarrow{AC'}=\overrightarrow{AF}+\overrightarrow{FC'}=\frac{1}{2}\overrightarrow{b}+\overrightarrow{FC'}\)
\(\overrightarrow{AA'}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DA'}=\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}+\overrightarrow{DA}\)
Do đó, điều phải chứng minh tương đương với
\(\overrightarrow{AB'}=\overrightarrow{FC'}=\overrightarrow{DA'}\)
Giả sử tam giác ABC định hướng dương. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{2}\) và
\(k=\cot\widehat{B'AC}=\cot\widehat{C'AB}\)
Ta có
\(f\left(\overrightarrow{EB'}+\overrightarrow{FC'}\right)=f\left(\overrightarrow{EB'}\right)+f\left(\overrightarrow{FC'}\right)\)
\(=k\overrightarrow{EA}+k\overrightarrow{AF}=\frac{k}{2}\left(\overrightarrow{b}-\overrightarrow{c}\right)\) (do \(\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BC}=0\) )
\(=\frac{k}{2}\overrightarrow{CB}=k\overrightarrow{DB}=f\left(\overrightarrow{DA'}\right)\)
Suy ra điều cần chứng minh
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông A. Về phía ngoài tam giác dựng hình chữ nhật BCDE có \(CD=\frac{BC}{\sqrt{2}}\).Gọi H,K lần lượt là giao điểm của ED với AB và AC. Gọi M,N lần lượt là giao điểm của BC với AC và AE. Chứng minh \(BC^2=BM^2+CN^2\)