Các câu hỏi tương tự
Cho một tam giác đều ABC cạnh A. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định giá trị lớn nhất của diện tích hình chữ nhật đó. B. 0
Đọc tiếp
Cho một tam giác đều ABC cạnh A. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định giá trị lớn nhất của diện tích hình chữ nhật đó.
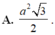
B. 0
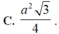
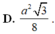
Cho tam giác đều ABC cạnh a. người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định vị trị của điểm M sao cho hình chữ nhật có diện tích lớn nhất và giá trị lớn nhất đó là.
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại A và có AB 4cm. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABC). Lấy M thuộc SC sao cho CM 2MS. Khoảng cách giữa hai đường AC và BM là
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại A và có AB = 4cm. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABC). Lấy M thuộc SC sao cho CM = 2MS. Khoảng cách giữa hai đường AC và BM là
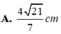
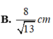
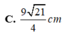

Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh a, tam giác A BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC. Tính cosin góc
α
giữa hai đường thẳng AA và BM.
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
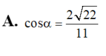
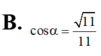
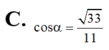
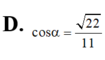
Trong không gian cho hai tam giác đều ABC và ABC’ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AC, CB, BC’, C’A. Tứ giác MNPQ là hình gì? A. Hình bình hành B. Hình chữ nhật C. Hình vuông D. Hình thang
Đọc tiếp
Trong không gian cho hai tam giác đều ABC và ABC’ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AC, CB, BC’, C’A. Tứ giác MNPQ là hình gì?
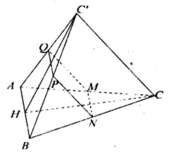
A. Hình bình hành
B. Hình chữ nhật
C. Hình vuông
D. Hình thang
Cho hình chóp tam giác S.ABC có SA vuông góc với mặt đáy, tam giác ABC cân tại A. Trên cạnh AB lấy điểm D sao cho AB = 3AD. Gọi H là hình chiếu của B lên CD, M là trung điểm CH. Tính theo a thể tích khối chóp S.ABM biết SA = AM = a và BM = 2/3 a
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0 x a) Mặt phẳng (
α
) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0 < x < a) Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
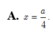
![]()
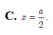
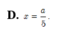
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0 x a). Mặt phẳng (
α
) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A. x
a
4
B. x
a
3
C. x
a
2
D. x ...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0 < x < a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0 x a). Mặt phẳng
(
α
)
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0 < x< a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
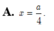
![]()
![]()