cho tam giác ABC nhọn biết ab<ac các đg cao BE ; CF cắt nhau tại H gọi M là trung điểm BC . Tu M ke tia doi voi MH sao cho MH = MK .
a )c/m tu giac BHCK la hình bình hành
b) c/m AB vuong BK
AC vuong KC
c) c/m tam giac FEM cân
cho tam giác nhọn abc .kẻ ah vuông góc bc .Biết AB = 13, AH = 12, HC = 16 .Tính chu vi tam giác ABC
* Tự vẽ hình nha !
Xét △AHB vuông tại H, ta có:
BH2 = AB2 - AH2 (Py-ta-go)
BH2 = 132 - 122 = 25
=> BH = √25 =5 (cm)
Xét △AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (Py-ta-go)
AC2 = 122 + 162 = 400
=> AC = √400 = 20 (cm)
Ta có: BC = BH + HC = 5 + 16 = 21 (cm)
Chu vi tam giác ABC:
AB + AC + BC = 13 + 20 + 21 = 54 (cm)
Vậy ....................
https://hoc247.net/hoi-dap/toan-7/tinh-chu-vi-tam-giac-abc-biet-ab-13cm-ah-12cm-va-hc-16cm-faq407733.html
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=AB^2-AH^2=13^2-12^2=25\)
hay HB=5(cm)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
hay AC=20(cm)
Ta có: HC+HB=BC(H nằm giữa B và C)
nên BC=16+5=21(cm)
Chu vi của tam giác ABC là:
AB+AC+BC=13+20+21=54(cm)
Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Tham khảo:
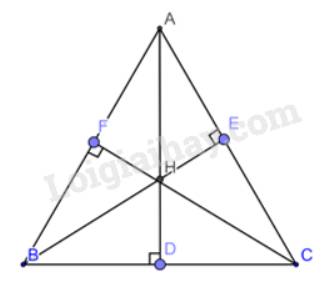
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau
1.Cho tam giác ABC nhọn, vẽ đường cao AH. Tính chu vu của tam giác ABC, biết AC = 13cm, AH = 12 cm, BH = 9cm
2. Cho tam giác ABC, góc A = 90 độ. BIết AB + AC = 49 cm; AB - AC = 7cm. Tínnh BC
3. Cho tam giác ABC, AB = AC =17 cm. Kẻ BD vuông góc với AC. Tính BC biết BD = 15cm
Cho tam giác ABC nhọn. Kẻ AH ^BC (HÎBC). Tính chu vi của tam giác ABC biết AB = 10cm, AH = 8cm, HC = 5cm.
AH vuông góc vs BC ( H thuocj BC ) nha
kẻ ah vuông góc vs bc ak
Cho tam giác ABC nhọn. kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AB = 5cm, AH = 4cm, HC = 12cm
Áp dụng định lý Pitago, ta có: \(AC^2=AH^2+HC^2\)
\(\Rightarrow20^2=12^2+HC^2\)
\(\Rightarrow HC^2=20^2-12^2\)
\(\Rightarrow HC^2=400-144=256\)
\(\Rightarrow HC=16\left(cm\right)\)
Áp dụng định lý Pitago, ta có: \(AB^2=BH^2+AH^2\)
\(\Rightarrow AB^2=5^2+12^2\)
\(\Rightarrow AB^2=25+144=169\)
\(\Rightarrow AB=13\left(cm\right)\)
Vậy CV tam giác ABC là
\(20+5+16+13=54\left(cm\right)\)
a) tính số đo mỗi góc nhọn của tam giác ABC vuông cân tại A
b) cho tam giác ABC . Biết AB=11cm;AC=15cm; BC=19cm
so sánh các góc của tam giác ABC
a, Do ABC vuông cân
=> Góc A = 90 độ
=> Góc B = Góc C = 90/2 = 45 độ
b, Do AB < AC < BC (11 < 15 < 19)
=> Góc C < Góc B < Góc A (Quan hệ góc đối diện)
Cho tam giác ABC nhọn . Kẻ AH vuông góc với BC. Tính chu vi của tam giác ABC . Biết AB = 5cm, AH=4cm, HC=12cm
Ta có:\(AC^2=HC^2+AH^2\)(Định lý pytago)
\(\Rightarrow AH^2=AC^2-HC^2=4^2-2^2=16-4=12\)
\(\Rightarrow AH=\sqrt{12}\approx3\)
Độ dài BC là :3+2=5
Chu vi của tam giác ABC la:\(4+5+5\approx14\)
CÁC BN THỬ VÀO TRANG CÁ NHÂN CỦA MIK ĐI, BẤT NGỜ LẮM
Tự vẽ hình nha
AH vg vs BC => Tam giác AHC và tam giác AHB v tại H
Áp dụng định lí pytago vào tam giác v AHC ta có:
\(AH^2+HC^2=AC^2\)
\(\Leftrightarrow\) \(12^2+16^2=AC^2\)
\(\Leftrightarrow\)\(AC^2=400\)
\(\Leftrightarrow\)\(AC=20cm\)
Áp dụng đlí pytago vào tam giác v AHB có:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow\)\(HB^2=AB^2-AH^2=13^2-12^2=25\)
\(\Rightarrow\)\(HB=5cm\)
Mà HB + HC = BC
=> BC = 5+16 = 21cm
Vậy AC = 20 cm và BC = 21 cm
cho tam giác nhọn ABC KẺ AH vuông góc BC.Tính chu vi tam giác biết AB=5cm,AH=4cm,HC=12cm
CHO tam giác nhọn ABC tính p của tam giác ABC biết AB bằng 5cm, AH bằng 4cm ,HC bằng 12CM kẻ AH vuông góc với BC