Cho \(\widehat{xOy}\).M là 1 điểm nằm trong góc. Vẽ MB,MC lần lượt vuông góc với Ox, Oy \(\left(B\in Ox;C\in Oy\right)\)sao cho MB=MC . Chứng minh \(M\in\)tia phân giác góc xOy

Những câu hỏi liên quan
1, cho xx'vuông góc với yy" tại O. Lấy điểm M nằm trong góc xOy. từ M vẽ MA vuông góc vs Ox tại A, MB vuông góc Oy tại B .Chứng minh MA vuông góc vs MB.
2 ,Cho góc xOy =90 độ .Lấy a nằm trong goc xOy .từ A vẽ AB vuông góc vs Ox (B thuộc Ox) ,AC vuông góc vs Oy (C thuộc Oy )
a, chứng minh AB // Oy
b, chứng minh góc OAB = AOC
Bài 1: Vẽ đường thẳng a và đường thẳng b sao cho a song song với b.Lấy điểm M nằm ngoài 2 đường thẳng a,b vẽ đường thẳng cđi qua M và vuông góc với a và b.Bài 2:Cho góc xOy và điểm M nằm trong góc đó qua M kẻ MA vuông góc với Ox cắt Oy tại C, kẻ MB vuông góc với Oy cắt Ox tại D.Từ D và C kẻ các tia vuông góc với Ox;Oy các tia này cắt Ox;Oy lần lượt tại E,F và cắt nhau tại N.Tìm các cặp góc có các cạnh tương ứng song song.
Đọc tiếp
Bài 1: Vẽ đường thẳng a và đường thẳng b sao cho a song song với b.Lấy điểm M nằm ngoài 2 đường thẳng a,b vẽ đường thẳng cđi qua M và vuông góc với a và b.
Bài 2:Cho góc xOy và điểm M nằm trong góc đó qua M kẻ MA vuông góc với Ox cắt Oy tại C, kẻ MB vuông góc với Oy cắt Ox tại D.Từ D và C kẻ các tia vuông góc với Ox;Oy các tia này cắt Ox;Oy lần lượt tại E,F và cắt nhau tại N.Tìm các cặp góc có các cạnh tương ứng song song.
Từ điểm M thuộc tia phân giác của góc nhọn xOy, kẻ MA, MB lần lượt vuông góc với Ox, Oy (A ∈ Ox, B ∈ Oy).
a) Vẽ hình ghi giả thiết kết luận
b) Chứng minh tam giác AOB cân
c) Qua điểm N nằm giữa O và M, kẻ đường thẳng vuông góc với OM, cắt Ox tại E, Oy tại F. Chứng minh AB//EF
b: Xét ΔOMA vuông tại A và ΔOMB vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
DO đó: ΔOMA=ΔOMB
Suy ra: OA=OB
hay ΔOAB cân tại O
c: Xét ΔOEF có
ON là đường cao
ON là đường phân giác
Do đó: ΔOEF cân tại O
Suy ra: OE=OF
Xét ΔOBA có
OE/OA=OF/OB
Do đó: EF//AB
Đúng 0
Bình luận (0)
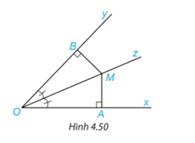
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
Đúng 1
Bình luận (0)
Cho góc xOz bằng 120 độ, Oy là tia phân giác của góc xOz, Ot là tia phân giác của góc xOy, M là điểm thuộc miền trong của focs yOz Vẽ MA vuông góc với Ox, vẽ MB vuông góc với Oy, vẽ MC vuông góc với Ot Tính độ dài OC theo Ma và Mb
Cho góc xOy=120 độ, Oy là tia phân giác của góc xOz , Ot là tia phân giác của góc xOy , M là điểm thuộc miền trong của góc yOz . Vẽ MA vuông góc Ox , vẽ MB vuông góc Oy , vẽ MC vuông góc Ot. Tính độ dài OC theo MA và MB.
cho góc xoy=50* và 1 điểm P nằm trong góc xoy. Từ P vẽ đường thẳng Py' song song với oy, Px' vuông góc với ox. Hai đường thẳng này cắt ox lần lượt tại N và M. Tính góc MPN.
ta thấy góc NPO = góc NOy = 50 độ ( so le )
xét tam giác vuông NMP có
góc NPO + góc MPN = 90 độ ( tính chất tam giác vuông )
=> góc MPN = 90 độ - góc NOP =90 độ - 50 độ =40 độ
Đúng 0
Bình luận (0)
BÀi 7: Vẽ hình theo diễn đạt sau:
Cho góc xOy và điểm M trong góc đó. Qua M kẻ MA vuông góc với Ox cắt Oy tại C, kẻ MB vuông góc với Oy cắt Ox tại D. Từ D và C kẻ các tia vuông góc với Ox, Oy, các tia này cắt Oy và Ox lần lượt tại E và F và cắt nhau tại N.
Vẽ góc xOy là 65°. M là một điểm bất kì nằm trong góc xOy. Vẽ MA vuông góc với Ox, A thuộc Ox; AB vuông góc với Oy, B thuộc Oy. Vẽ đường thẳng d qua M và song song với Oy.
Xem chi tiết















