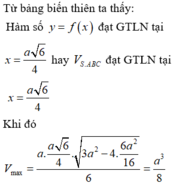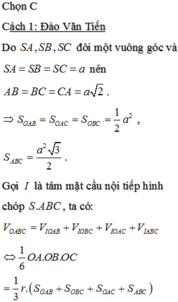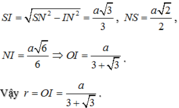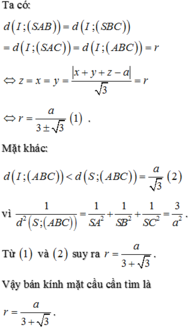Cho hình chóp S.ABC trong đó SA; AB; BC vuông góc với nhau từng đôi một. Biết S A = a 3 , A B = a 3 . Khoảng cách từ A đến (SBC) bằng:

Những câu hỏi liên quan
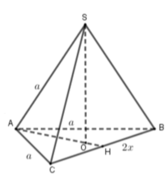
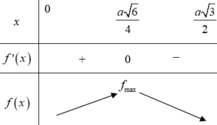
Cho hình chóp S.ABC có SASBSCABACa, BC2x (trong đó a là hằng số và x thay đổi thuộc khoảng
0
;
a
3
2
. Tính thể tích lớn nhất Vmax của hình chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=2x (trong đó a là hằng số và x thay đổi thuộc khoảng 0 ; a 3 2 . Tính thể tích lớn nhất Vmax của hình chóp S.ABC
![]()
![]()
![]()
![]()
có nge9ejr 0 uiwu3433r2///3
Cho hình chóp S.ABC có SASBSCABACa, BC2x (trong đó a là hằng số và x thay đổi thuộc khoảng
0
;
a
3
2
). Tính thể tích lớn nhất
V
m
a
x
của hình chóp S.ABC A.
V
m
a...
Đọc tiếp
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=2x (trong đó a là hằng số và x thay đổi thuộc khoảng 0 ; a 3 2 ). Tính thể tích lớn nhất V m a x của hình chóp S.ABC
A. V m a x = a 3 6
B. V m a x = a 3 2 4
C. V m a x = a 3 8
D. V m a x = a 3 2 12
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc và SASBSCa. Tính bán kính r của mặt cầu nội tiếp hình chóp S.ABC (mặt cầu nội tiếp hình chóp là mặt cầu tiếp xúc với tất cả các mặt của hình chóp và có tâm nằm trong hình chóp).
Đọc tiếp
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc và SA=SB=SC=a. Tính bán kính r của mặt cầu nội tiếp hình chóp S.ABC (mặt cầu nội tiếp hình chóp là mặt cầu tiếp xúc với tất cả các mặt của hình chóp và có tâm nằm trong hình chóp).
![]()
![]()
![]()
Cho hình chóp S.ABC trong đó SA, AB, BC vuông góc với nhau từng đôi một. Biết
S
A
A
B
a
3
. Khoảng cách từ A đến (SBC) bằng: A.
a
3
2
B.
a
2
3
C.
2
a...
Đọc tiếp
Cho hình chóp S.ABC trong đó SA, AB, BC vuông góc với nhau từng đôi một. Biết S A = A B = a 3 . Khoảng cách từ A đến (SBC) bằng:
A. a 3 2
B. a 2 3
C. 2 a 5 5
D. a 6 2
Chọn D.
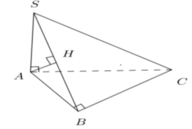
- Kẻ AH ⊥ SB.
- Ta có:
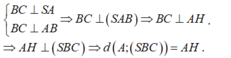
- Trong tam giác vuông SAB ta có:
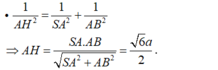
Đúng 0
Bình luận (0)
Cho hình chóp
S
.
A
B
C
trong đó
S
A
,
A
B
,
B
C
vuông góc với nhau từng đôi một. Biết
S
A
3
a
,
A
B
a
3
,
B
C
a
6
.
Khoảng cách từ B đến SC bằng: A.
2...
Đọc tiếp
Cho hình chóp S . A B C trong đó S A , A B , B C vuông góc với nhau từng đôi một. Biết S A = 3 a , A B = a 3 , B C = a 6 . Khoảng cách từ B đến SC bằng:
A. 2 a 3
B. a 3
C. a 2
D. 2 a
Đáp án là A
Kẻ B H ⊥ S C ⇒ d B ; S C = B H .
Ta có: B C ⊥ S A B C ⊥ A B ⇒ B C ⊥ S A B ⇒ B C ⊥ S B
Do đó: 1 B H 2 = 1 B C 2 + 1 B S 2 = 1 B C 2 + 1 B A 2 + S A 2 = 1 6 a 2 + 1 9 a 2 + 3 a 2 = 1 4 a 2
⇒ B H = 2 a ⇒ d B ; S C = 2 a .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SA ⊥ (ABC), đáy ABC là tam giác đều. Tính thể tích khối chóp S.ABC biết AB a; SA a. A.
a
3
3
12
B.
a
3
3
4
C.
a
3
D.
a
3...
Đọc tiếp
Cho hình chóp S.ABC có SA ⊥ (ABC), đáy ABC là tam giác đều. Tính thể tích khối chóp S.ABC biết AB = a; SA = a.
A. a 3 3 12
B. a 3 3 4
C. a 3
D. a 3 3
Chọn A.
Do đáy là tam tam giác đều cạnh a nên diện tích đáy là:
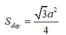
Thể tích khối chóp là:
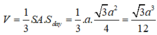
Đúng 0
Bình luận (0)
Cho hình chóp
S
.
A
B
C
có
S
A
⊥
(
A
B
C
)
,
S
A
a
3
. Tam giác ABC vuông cân tại B,
A
C
2
a
. Thể tích khối chóp
S
.
A
B
C
bằng. A.
a
3
3
B.
a
3...
Đọc tiếp
Cho hình chóp S . A B C có S A ⊥ ( A B C ) , S A = a 3 . Tam giác ABC vuông cân tại B, A C = 2 a . Thể tích khối chóp S . A B C bằng.
A. a 3 3
B. a 3 3 6
C. 2 a 3 3 2
D. a 3 3 3
Đáp án là D

• Trong tam giác ABC vuông cân tại B có: A B = B C = A C 2 = a 2
• Đường cao hình chóp: S A = a 3 .Diện tích đáy S ∆ A B C = 1 2 A B . B C = a 2 .
• Thể tích khối chóp: S S . A B C = 1 3 S A S ∆ A B C = a 8 3 3 .
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có cạnh đáy AB=12cm, cạnh bên SA=10cm. Tính diện tích xung quanh của hình chóp đều đó
Lời giải:
Xét tam giác $SAB$ có $SA=SB=10$, $AB=12$
Kẻ $SH\perp AB$ thì $H$ là trung điểm của $AB$.
$\Rightarrow AH=6$ (cm)
Theo định lý Pitago:
$SH=\sqrt{SA^2-AH^2}=\sqrt{10^2-6^2}=8$ (cm)
$S_{SAB}=\frac{SH.AB}{2}=\frac{8.12}{2}=48$ (cm vuông)
$S_{xq}=3S_{SAB}=3.48=144$ (cm vuông)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABC có
S
A
⊥
(
A
B
C
)
,
S
A
2
a
tam giác ABC cân tại A,
B
C
2
a
2
,
cos
A
C
B
^
1
3
. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC A. ...
Đọc tiếp
Cho hình chóp S.ABC có S A ⊥ ( A B C ) , S A = 2 a tam giác ABC cân tại A, B C = 2 a 2 , cos A C B ^ = 1 3 . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
A. S = 97 πa 2 3
B. S = 97 πa 2 4
C. S = 97 πa 2 2
D. S = 97 πa 2 5
Đáp án B
Gọi H là trung diểm của BC suy ra cos A C B ^ = sin H A B ^ = 1 3 ⇒ cos H A B ^ = 2 2 3
Mà sin B A C ^ = 2 sin H A B ^ . cos H A B ^ = 4 2 9 nên theo định lí Sin, ta có R ∆ A B C = B C 2 s i n B A C ^ = 9 4
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là R = R 2 ∆ A B C + S A 2 4 = a 97 4
Vậy diện tích mặt cầu cần tính là S = 4 πR 2 = 4 π a 97 4 2 = 97 πa 2 4
Đúng 0
Bình luận (0)