a. A=1/51+1/52+1/53+...+1/100; B=1/1.2+1/3.4+...+1/99.100

Những câu hỏi liên quan
Tính A:
A=1/51 + 1/52 + 1/53 + ......... + 1/100
\(A=\dfrac{1}{51}+\dfrac{1}{52}+\dfrac{1}{53}+...+\dfrac{1}{100}\)
Tham khảo: (mk chx chắc lắm đâu nha)
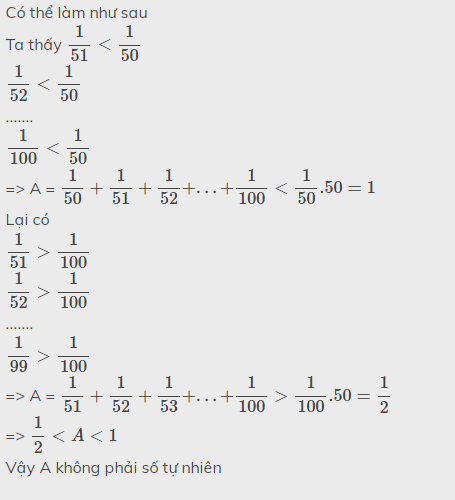
Đúng 0
Bình luận (0)
Tính A=1/51+1/52+1/53+...+1/99+1/100
Tính A:
A=1/51 + 1/52 + 1/53 + ......... + 1/100
Có lẽ ý bạn là CM :A = 1-1/2+1/3-1/4+...+1/99-1/100 phải không ?
Bài này thì ta dùng hệ thức A- B = A + B - 2B
Xét vế phải, ta có:
1 - 1/2 + 1/3 - 1/4 + ... + 1/99 - 1/100
= (1 + 1/3 + 1/5 + ... +1/99) - (1/2+ 1/4 + 1/6 + ... + 1/100)
= (1 + 1/3 + 1/5 + ... + 1/99) + (1/2 + 1/4 + 1/6 + ... + 1/100)
- 2(1/2 + 1/4 + 1/6 + ... + 1/100)
=(1 + 1/2 + 1/3 + 1/4 + ... + 1/100) - (1 + 1/2 + 1/3 +... + 1/50)
=1/51 + 1/52 +1/53 + ... + 1/100
Vế phải bằng về trái
--> Đẳng thức được chứng minh
Đúng 0
Bình luận (1)
Chứng tỏ A = 1/51 + 1/52 + 1/53 + .....+1/99 + 1/100 <1/2
Đề sai tại vì:
Ta thấy từ: \(\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+...+\frac{1}{99}\) mỗi số hạng đều lớn hơn \(\frac{1}{100}\)
Mà tổng trên có : ( 100 - 51 ) + 1 = 50 ( số hạng )
Nên:
\(\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+...+\frac{1}{99}+\frac{1}{100}>\frac{1}{100}.50=\frac{50}{100}=\frac{1}{2}\)
Vậy : \(A>\frac{1}{2}\)
Đúng 0
Bình luận (0)
A= 1/51+1/52+1/53+...+1/99+1/100. so sánh với 1/2 và 1
so sánh A và B . biết A= 1/1.2 + 1/3.4 + 1/5.6 + ......+ 1 / 99.100
B = 2021/ 51 + 2021/52 + 2021/53 + .... + 2021/100
so sánh A và B . biết A= 1/1.2 + 1/3.4 + 1/5.6 + ......+ 1 / 99.100
B = 2021/ 51 + 2021/52 + 2021/53 + .... + 2021/100
=> A < B
chắc vại-.-
tui hok giỏi toán lém
Cho A = 1/51 + 1/52+ 1/53 +...+ 1/100
B = 1/1.2 + 1/3.4 +1/5.6+...+ 1/99.100
A/ B = ?
xét B ta có:
B=1/1.2+1/3.4+1/5.6+...+1/99.100
B=1-1/2+1/3-1/4+1/5-1/6+...+1/99-100
B=(1+1/3+1/5+...+1/99)-(1/2+1/4+...+1/100)
B=(1+1/3+1/5+...+1/99)+(1/2+1/4+1/6+...+1/100)-2(1/2+1/4+1/6+...+1/100)
B=(1+1/2+1/3+...+1/99+1/100)-(1+1/2+1/3+1/4+...+1/50)
=>B=1/51+1/52+1/53+...+1/100
=>A/B=1/51+1/52+...+1/100:1/51+1/52+...+1/100=1 (đpcm)
Đó là cách nhanh nhất để giải nếu bn ko hỉu thì mik sẽ giải chi tiết cho
chúc bn học tốt ^-^
Đúng 0
Bình luận (0)

















