Cho tam giác ABC có AB=3;AC=4;BC=5
a/ tam giác ABC là tam giác gì?
b/ Trên tia đối tia AB lấy M sao cho KM=AC. Trong đó AC lấy N sao cho AN=HB. Chứng minh BC=MN và NB//MC
c/ I là trung điểm MC. Chứng minh tam giác BIN cân
Những câu hỏi liên quan
1 ) Cho tam giác ABC có góc A nhọn , AB=4 , AC=5 và diện tích tam giác ABC =8 . Tính BC
2 ) Cho tam giác ABC có AB=3 , góc ACB = 45° , góc ABC = 60° . Tính BC
em mới học lớp 7 hà
năm nay lên lớp 8 =)))))
Đúng 0
Bình luận (0)
1)Ta có: \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
\(\Leftrightarrow8=\dfrac{1}{2}\times4\times5\times sinA\)
\(\Leftrightarrow\sin A=0,8\)
Lại có: \(\left(\sin A\right)^2+\left(\cos A\right)^2=1\Leftrightarrow\cos A=0,6.\)
Áp dụng định lí hàm số cosin:
\(BC^2=AB^2+AC^2-2AB\times AC\times\cos A\)
\(\Leftrightarrow BC^2=4^2+5^2-2\times4\times5\times0,6=17\)
\(\Leftrightarrow BC=\sqrt{17}.\)
2) Trong \(\Delta ABC\) có: \(g\text{ó}cA+g\text{óc}B+g\text{óc}C=180^o\)
=> BAC=75o.
Áp dụng định lí hàm số sin:
\(\dfrac{AB}{\sin C}=\dfrac{BC}{\sin A}\Leftrightarrow\dfrac{3}{\sin45^o}=\dfrac{BC}{\sin75^o}\)
\(\Leftrightarrow BC=\dfrac{3+3\sqrt{3}}{2}\).
Đúng 0
Bình luận (0)
Bài 1:Cho tam giác ABC có A80 độ,B40 độ.Tia phân giác của góc C cắt AB tại D.Tính số đo góc CDA;CDB.Bài 2:Cho tam giác ABCtam giác DEF có AB3cm,DF 4cm,EF5cm.Tính chu vi của mỗi tam giác.Bài 3:Cho tam giác ABC có ABAC,D là trung điểm của BC(D thuộc BC).Chứng minh:a)Tam giác ABD tam giác ACD b)BADCAD c)AD vuông góc BCLƯU Ý:NHỮNG BÀI TRÊN KO CÓ BÀI NÀO CÓ HÌNH CẢ
Đọc tiếp
Bài 1:Cho tam giác ABC có A=80 độ,B=40 độ.Tia phân giác của góc C cắt AB tại D.Tính số đo góc CDA;CDB.
Bài 2:Cho tam giác ABC=tam giác DEF có AB=3cm,DF= 4cm,EF=5cm.Tính chu vi của mỗi tam giác.
Bài 3:Cho tam giác ABC có AB=AC,D là trung điểm của BC(D thuộc BC).Chứng minh:
a)Tam giác ABD= tam giác ACD b)BAD=CAD c)AD vuông góc BC
LƯU Ý:NHỮNG BÀI TRÊN KO CÓ BÀI NÀO CÓ HÌNH CẢ
Bài 3:
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD
b: Ta có: ΔABD=ΔACD
nên \(\widehat{BAD}=\widehat{CAD}\)
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao
Đúng 0
Bình luận (0)
Bài 2 : Cho tam giác ABC có AB3cm; AC 4cm; BC 5cm . So sánh các góc của tam giác ABCBài 3 :Cho tam giác ABC có góc B60 độ ; góc C 40 độ . So sánh các cạnh của tam giác ABCBài 4 : Cho tam giác ABC có AB5cm ; AC 12 cm ; BC13 cma) Tam giác ABC là tam giác gì ?b) So sánh các góc của tam giác ABCBài 5 : Cho tam giác ABC vuông tại A có AB10cm ; AC 24 cma) Tính độ dài cạnh BC?b) Tam giác ABC là tam giác gì ?
Đọc tiếp
Bài 2 : Cho tam giác ABC có AB=3cm; AC= 4cm; BC= 5cm . So sánh các góc của tam giác ABC
Bài 3 :Cho tam giác ABC có góc B=60 độ ; góc C = 40 độ . So sánh các cạnh của tam giác ABC
Bài 4 : Cho tam giác ABC có AB=5cm ; AC= 12 cm ; BC=13 cm
a) Tam giác ABC là tam giác gì ?
b) So sánh các góc của tam giác ABC
Bài 5 : Cho tam giác ABC vuông tại A có AB=10cm ; AC= 24 cm
a) Tính độ dài cạnh BC=?
b) Tam giác ABC là tam giác gì ?
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
Đúng 0
Bình luận (0)
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
BÀI TẬP
Bài 1. Cho tam giác ABC có AB=5cm; AC=7cm. So sánh <B và <C
Bài 2. Cho tam giác ABC có AB=3cm; AC= 4cm;BC = 5cm. So sánh các góc của
tam giác
Bài 3.Cho tam giác có <B=60 0 ; <C =40 0 . So sánh các cạnh của tam giác ABC
Bài 4. Cho tam giác ABC vuông ở A có AB= 6cm; BC = 10 cm
1/ Tính AC
2/ So sánh các góc của tam giác ABC
cho tam giác abc vuông ở A có chu vi = 24m có cạch ab = 3/4 ac ,ab= 10m .Tính diện tích tam giác abc.
Tổng độ dài hai cạnh AB và AC là :
24 - 10 = 14 ( cm )
Độ dài cạnh AB là :
14 : ( 3 + 4 ) x 3 = 6 ( cm )
Độ dài cạnh AC là :
14 - 6 = 9 ( cm )
Diện tích hình tam giác ABC là :
6 x 9 : 2 = 27 ( cm2)
Đáp số : 27 cm2
Đúng 0
Bình luận (0)
tổng độ dài hai cạnh là
24-10=14 cm
độ dại cạnh AB là
14:(3+4).3=6 cm
độ dài cạnh AC là
14-6=8 cm
diện tích là
6.7:2=27cm2
đáp số...............
Đúng 0
Bình luận (0)
Thảo Mai bạn tham khảo đây nhé:
Câu hỏi của Tran Quynh Anh - Toán lớp 5 - Học toán với OnlineMath
......
Thảo Mai
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC có 3 đường cao AB=BE=CF . Chứng minh rằng khi đó tam giác ABC là tam giác đều
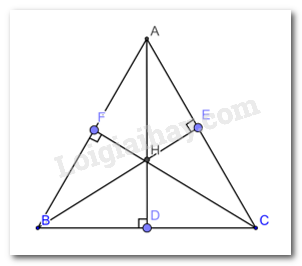
Xét tam giác BFC vuông tại F và tam giác BEC vuông tại E có :
BC chung
FC = BE
=> Tam giác BFC= Tam giác BEC(ch-cgv)
=> Góc C= Góc B( 2 góc tương ứng) (1)
Xét tam giác CFA vuông tại F và tam giác ADC vuông tại D ta có :
CF = AD
AC chung
=> Tam giác CFA= Tam giác ADC(ch-cgv)
=> Góc C= Góc A( 2 góc tương ứng) (2)
Từ (1) và (2) suy ra Góc C= Góc A= Góc B
Vậy Tam Giacs ABC là tam giác đều
Đúng 2
Bình luận (0)
Bài 3:Cho tam giác ABC có AB=8,AC=10,BC=13.Tam giác ABC có góc tù hay không ?
\(\cos A=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{8^2+10^2-13^2}{2\cdot8\cdot10}=-\dfrac{1}{32}< 0\)
nên \(\widehat{A}>90^0\)
=>ΔABC tù
Đúng 0
Bình luận (0)
28 tháng 2 2022 lúc 10:15
Bài1 Cho tam giác ABC. P trên AB sao cho PB 2 3 PA. Q là trung điểm của BC. a So sánh diện tích tam giác PQC với diện tích tam giác ABC. b Biết diện tích tam giác PQC 12dm 2. Tính diện tích tam giác ABC. Bài2 Cho tam giác ABC. M và N lần lượt trên AB và BC sao cho AM 1 3 AB, AN 1 3 AC. BN cắt CM tại K. So sánh diện tích BKM với CKN. Có vẽ hình
Xem chi tiết
a) Diện h tam giác ABC là :
7,2 x 7,5 : 2 = 27 ( cm2 )
b) Nối P với C
Xét hai tam giác APC và ABC
Chung chiều cao hạ từ đỉnh C xuống cạnh AB
PA = 2/3 AB
=> SAPC = SABC x 2/3 = 27 x 2/3 = 18 ( cm2 )
Xét 2 tam giác APQ và APC
Chung chiều cao hạ từ đỉnh P xuống cạnh AC
AQ = 1/4 AC
=> SAPQ = SAPC X 1/4 = 18 x 1/4 = 4,5 ( cm2 )
Đáp số : 4,5 cm2
bn wiiiiiiiii có đúng ko zậy
a) Diện h tam giác ABC là :
7,2 x 7,5 : 2 = 27 ( cm2 )
b) Nối P với C
Xét hai tam giác APC và ABC
Chung chiều cao hạ từ đỉnh C xuống cạnh AB
PA = 2/3 AB
=> SAPC = SABC x 2/3 = 27 x 2/3 = 18 ( cm2 )
Xét 2 tam giác APQ và APC
Chung chiều cao hạ từ đỉnh P xuống cạnh AC
AQ = 1/4 AC
=> SAPQ = SAPC X 1/4 = 18 x 1/4 = 4,5 ( cm2 )
Đáp số : 4,5 cm2
꧁༺๖ۣ๖ۣۜSkyღ๖ۣۜlạnh☯๖ۣۜlùngɠɠ༻꧂
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 1: Tam giác DEF vuông tại D có tổng hai góc nhọn E và F bằng : ......
Câu 2: Cho tam giác ABC có AB=AC , M là trung điểm của BC thì ta có 2 tam giác bằng nhau là : .....
Câu 3: Cho tam giác ABC và tam giác MNP có AB =MN , góc A = góc M . Để tam giác ABC = tam giác MNP thao trường hợp (c.g.c) thì cần thêm điều kiện là:....
câu 1 E + F = 90 độ
câu 2 góc AMB và góc AMC
câu 3 AC = MP
Đúng 0
Bình luận (0)
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (1)