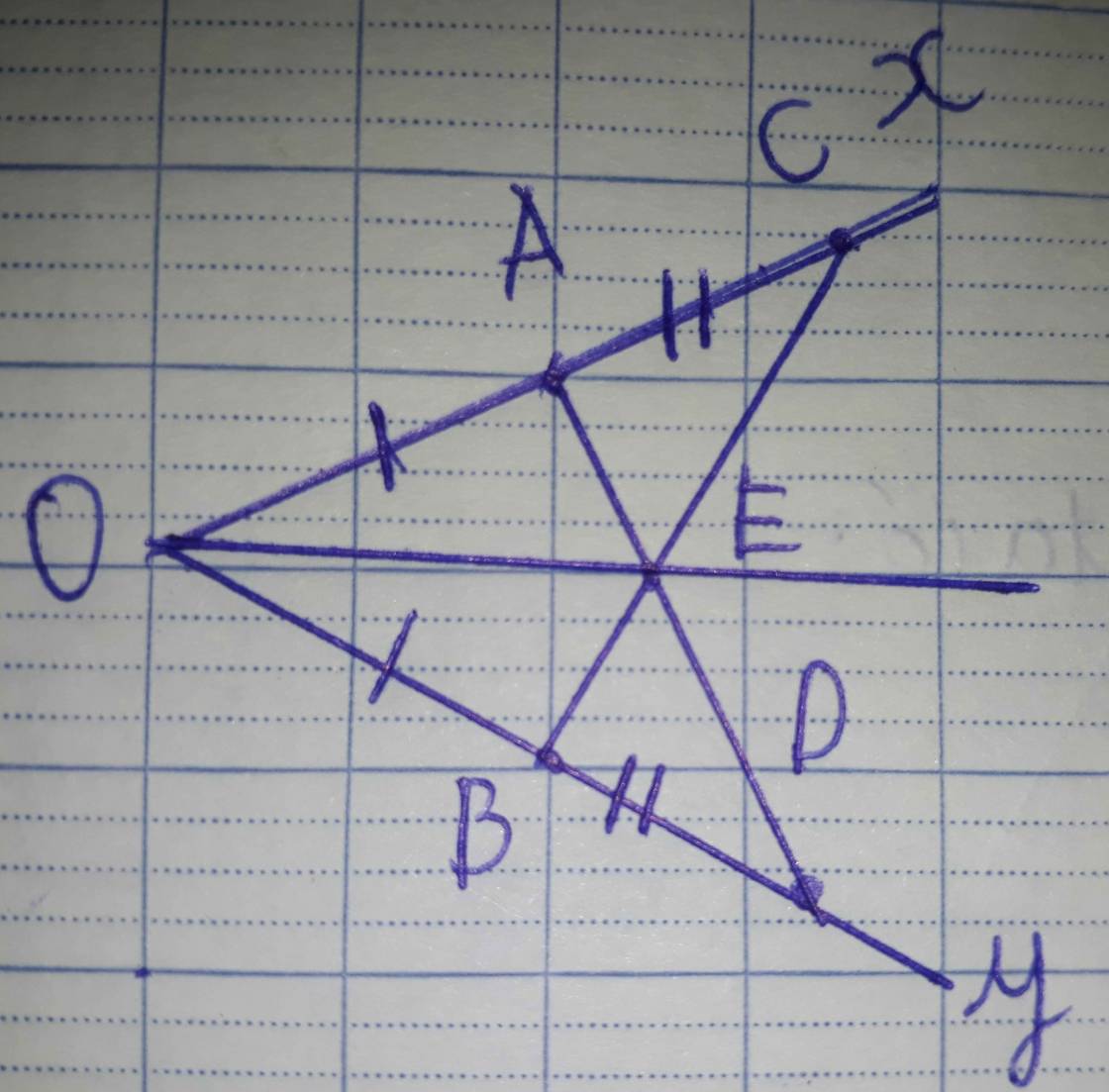
a) xét ΔOCB và ΔODA, ta có :

OA = OB (giả thiết)

\(\widehat{O}\) là góc chung

AC = BD (giả thiết)

⇒ ΔOCB = ΔODA (c.g.c)

⇒ AC = BD (2 cạnh tương ứng)

b) xét ΔEAC và ΔEBD, ta có : 

AD = BC (câu a)

\(\widehat{AEC}=\widehat{BED}\) (vì là 2 góc đối đỉnh) 

AC = BD (giả thiết)

⇒ ΔEAC = ΔEBD (C.G.C)

c) xét ΔOAE và ΔOBE, ta có :

OA = OB (giả thiết)

AE = BE [vì ΔEAC = ΔEBD (2 cạnh tương ứng)]

OE là cạnh chung

⇒ ΔOAE = ΔOBE (c.c.c)

⇒ \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)

a) bc\(^2\)= ab\(^2\)+ bc\(^2\)= 16+16=32

=> bc=\(\sqrt{32}\)

b) Xét tam giác ABD vuông tại D và tam giác ACD vuông tại D có:

Cạnh huyền AB=AC (tam giác ABC vuông cân tại A)

Góc nhọn B=C (tam giác ABC vuông cân tại A)

Do đó ABD=ACD (cạnh huyền-góc nhọn)

=>BD=CD (2 cạnh tương ứng)

=> D là trung điểm của BC

c)Ta có:

AB vuông góc với AC (gt)

DE vuông góc với AB (gt)

=> AC//DE

=> Góc DCA+EDC= 180\(^0\) (2 góc trong cùng phía)

=> EDA+ADC+DCA=180\(^0\)

Mà ADC=90\(^0\)

Nên EDA+DCA=90\(^0\)

Ta có: Tam giác ABC vuông cân tại A

=>ABC+ACB=90\(^0\)

mà ABC+BAD=90\(^0\)(tam giác ABD vuông tại D)

nên ACB=BAD

=> BAD=ABC (1)

Ta có: ABC+BDE=90\(^0\)

Mà BDE+EDA=90\(^0\)

Nên ABC=EDA (2)

Từ (1) và (2) suy ra: BAD=EDA

Tam giác AED có: BAD=EDA

                            DEA=90\(^0\)

Do đó tam giác ADE vuông cân tại E

Xét hình thang ABCD có:

AE = DE

BF = CF

=> EF là đường trung bình của hình thang ABCD

=> EF// AB và DC (1)

Mà : K ∈ EF (2)

Từ (1), (2) => EK // DC

Xét tam giác ADC có

AE = DE

EK// DC

=> AK = CK

Xét hình thang ABCD có 

E là trung điểm của AD

F là trung điểm của BC

Do đó: EF là đường trung bình của hình thang ABCD

Suy ra: \(FE=\dfrac{AB+CD}{2}\)

Tham khảo đây nha:

https://hoidap247.com/cau-hoi/1107494

E,F là trung điểm của AD và BC

=>  EF là đường trung bình của hình thang ABCD

=> \(EF=\dfrac{AB+CD}{2}\)