Cho hàm sốf (x) có đạo hàm trên [1;4] và f(1), f(4) = 10.Giá trị của I = ∫ 1 4 f ' ( x ) d x là
A. I = 12
B. I = 48
C. I = 8
D. I = 3
Cho hàm sốf (x) có đạo hàm với mọi x và thỏa mãn f(2x) = 4cosx.f(x) – 2x. Giá trị f’(0) là
A. 1
B. 3
C. 0
D. - 2
Đáp án A
Phương pháp: Đạo hàm hàm hợp: ![]()
Cách giải: Ta có: ![]()
=> ![]()
![]()
![]()
Cho hàm sốf(x) liên tục trên R. Biết ∫ 0 1 f ( x ) d x = 1 và ∫ 3 1 f ( x ) d x = 2 .Giá trị của ∫ 0 3 f ( x ) d x là
A. 2
B. 16
C. -1
D. -4
Câu 5. Cho hàm số f x có đạo hàm liên tục tên R và có đạo hàm ' 2 f x x x 9 1 .Tìm m để hàm số 2 y f x x m 2 đồng biến trên 1,3
Cho hàm số f x = sin x + x - 1 . Xét hai khẳng định sau
(1)Hàm số trên có đạo hàm tại x=1
(2)Hàm số liên tục tại x=1
Trong hai khẳng định trên
A. Chỉ có (1) đúng
B.Chỉ có (2) đúng
C. Cả hai đều đúng
D. Cả hai đều sai
Cho hàm số \(y = {x^{22}}\)
a) Tính đạo hàm của hàm số trên tại điểm x bất kì
b) Tính đạo hàm của hàm số trên tại điểm \({x_0} = - 1\)
a) Ta có: \(f'\left( x \right) = \left( {{x^{22}}} \right)' = 22.{x^{21}}\)
b) Đạo hàm của hàm số tại điểm \({x_0} = - 1\) là: \(f'\left( { - 1} \right) = 22.{\left( { - 1} \right)^{21}} = - 22\)
Cho hàm số f(x)=sinx+|x-1| Xét hai khẳng định sau
(1)Hàm số trên có đạo hàm tại ![]()
(2)Hàm số liên tục tại ![]() Trong hai khẳng định trên
Trong hai khẳng định trên
A. Chỉ có (1) đúng
B.Chỉ có (2) đúng
C.Cả hai đều đúng
D. Cả hai đều sai.
Cho hàm số y= f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm f’(x) .
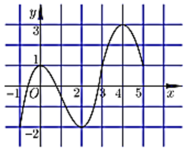
Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng
A (-3 ; -2)
B. (- 2 ; -1)
C. (- 1 ; 0)
D. (0 ; 2)
Cho hàm số y=f(x) liên tục trên R, có đạo hàm f'(x)= x ( x - 1 ) 2 ( x + 1 ) 2 . Hàm số đã cho có bao nhiêu điểm cực trị
A. Có đúng 3 điểm cực trị
B. Không có điểm cực trị
C. Có đúng 1 điểm cực trị
D. Có đúng 2 điểm cực trị
Cho hàm số y = f(x) có đạo hàm f ' x = x 2 x 2 - 1 , ∀ x ∈ ℝ . Hàm số y = 2 f - x đồng biến trên khoảng
A. 2 ; + ∞
B. - ∞ ; - 1
C. (-1;1)
D. (0;2)