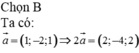Trong không gian Oxyz cho vectơ \(\overrightarrow{a}=\left(1;-3;4\right)\)
a) Tìm \(y_0\) và \(z_0\) để cho vectơ \(\overrightarrow{b}=\left(2;y_0;z_0\right)\) cùng phương với \(\overrightarrow{a}\)
b) Tìm tọa độ của vectơ \(\overrightarrow{c}\) biết rằng \(\overrightarrow{a}\) và \(\overrightarrow{c}\) ngược hướng và \(\left|\overrightarrow{c}\right|=2\left|\overrightarrow{a}\right|\)