Cho tam giác ABC có diện tích \(S=8\), hai đỉnh \(A\left(1;-2\right);B\left(2;3\right)\)
Tìm tọa độ đỉnh C, biết đỉnh C, biết rằng đỉnh C nằm trên đường thẳng \(d:2x+y-2=0\)
Những câu hỏi liên quan
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng
60
0
. Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy ngoại tiếp tam giác ABC bằng
Đọc tiếp
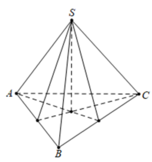
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng 60 0 . Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy ngoại tiếp tam giác ABC bằng
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng
S
A
B
và
A
B
C
bằng
60
°
. Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy ngoại tiếp tam giác ABC bằng A.
7
π
a...
Đọc tiếp
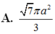
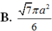
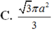
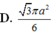
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng S A B và A B C bằng 60 ° . Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy ngoại tiếp tam giác ABC bằng
A. 7 π a 2 3
B. 7 π a 2 6
C. 3 π a 2 3
D. 3 π a 2 6
Cho tam giác đều ABC cạnh a. Tam giác
A
1
B
1
C
1
có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác
A
2
B
2
C
2
có các đỉnh là trung điểm các cạnh của tam giác
A
1
B
1
C...
Đọc tiếp
Cho tam giác đều ABC cạnh a. Tam giác A 1 B 1 C 1 có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A 2 B 2 C 2 có các đỉnh là trung điểm các cạnh của tam giác A 1 B 1 C 1 , …, tam giác A n + 1 B n + 1 C n + 1 có các đỉnh là trung điểm các cạnh của tam giác A n B n C n , …. Gọi S 1 , S 2 ,..., S n ,... theo thứ tự là diện tích các tam giác A 1 B 1 C 1 , A 2 B 2 C 2 , …, A n B n C n , … . Tìm tổng S = S 1 + S 2 + ... + S n + ...
A. S = a 2 3 3
B. S = a 2 3 8
C. S = a 2 3 12
D. S = a 2 3 16
Đáp án C
Dựa vào dữ kiện đề bài ta có thể suy ra tổng S là tổng của cấp số nhân lùi vô hạn với công bội
q = 1 4 ⇒ S = S 1 1 − q = a 3 3 4 . 1 4 1 − 1 4 = a 2 3 12
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh a. Tam giác
A
1
B
1
C
1
có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác
A
2
B
2
C
2
có các đỉnh là trung điểm các cạnh của tam giác
A
1
B
1
C...
Đọc tiếp
Cho tam giác đều ABC cạnh a. Tam giác A 1 B 1 C 1 có cách đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A 2 B 2 C 2 có các đỉnh là trung điểm các cạnh của tam giác A 1 B 1 C 1 , …, tam giác A n + 1 B n + 1 C n + 1 có các đỉnh là trung điểm các cạnh của tam giác A n B n C n , …. Gọi S 1 , S 2 , ... , S n , ... theo thứ tự là diện tích các tam giác A 1 B 1 C 1 , A 2 B 2 C 2 , …, A n B n C n , … . Tìm tổng S = S 1 + S 2 + ... + S n + ...
A. S = a 2 3 3
B. S = a 2 3 8
C. S = a 2 3 12
D. S = a 2 3 16
Đáp án C
Dựa vào dữ kiện đề bài ta có thể suy ra tổng S là tổng của cấp số nhân lùi vô hạn với công bội q = 1 4 ⇒ S = S 1 1 − q = a 3 3 4 . 1 4 1 − 1 4 = a 2 3 12
Đúng 0
Bình luận (0)
cho tam giác ABC có một cạnh bằng 60 cm và chu vi bằng 160cm . Tìm độ dài hai cạnh còn lại để tam giác ABC có diện tích lớn nhất(cho biết diện tích tam giác có độ dài ba cạnh là a,b,c có thể tính bằng công thức sau:
S=\(\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)_{ }}\);p=(a+b+c):2
a = 60cm
p = 160/2 = 80cm
p = \(\dfrac{a+b+c}{2}\) (1) => \(\dfrac{2p-a}{2}\) = \(\dfrac{b+c}{2}\)
Vì a, p là 1 hằng số nên để S đạt GTLN <=> (p-b) và (p-c) đạt GTLN
Áp dụng bđt Cosin, ta có:
\(\sqrt{\left(p-b\right)\left(p-c\right)}\) <= \(\dfrac{p-b+p-c}{2}\) = \(\dfrac{2p-b-c}{2}\)
=> \(\dfrac{S}{\sqrt{p\left(p-a\right)}}\) <= \(p-\dfrac{b+c}{2}\) = \(p-\dfrac{2p-a}{2}\) = \(\dfrac{a}{2}\)
=> 2S <= \(a\sqrt{p\left(p-a\right)}\) = \(60\sqrt{80.\left(80-60\right)}\) = 2400
=> S <= 1200 (\(cm^2\))
Dấu "=" xảy ra
<=> \(p-b\) = \(p-c\)
<=> b = c
Thay b = c vào (1), ta được:
p = \(\dfrac{a+2b}{2}\) => 80 = \(\dfrac{60+2b}{2}\) => b = c = 50 (cm)
=> đpcm
Đúng 0
Bình luận (0)
Cho tam giác ABC có CosB=1/3 , AC=b đường cao hạ từ đỉnh B bằng tổng hai đường cao còn lại . Tính diện tích của tam giác ABC
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJSABI+SCBJBài 3: Cho tam giác ABC có AB3cm, BC4cm, CA5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tí...
Đọc tiếp
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?
Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJ=SABI+SCBJ
Bài 3: Cho tam giác ABC có AB=3cm, BC=4cm, CA=5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tính diện tích mỗi phần?
Bài 4: Cho tam giác ABC có diện tích 30cm2. trên cạnh AB lấy điểm D sao cho AD=2DB, trên cạnh AC lấy điểm E sao cho AE=3EC. Gọi M là giao điểm của BE và CD. Tính diện tích tam giác AMB?
Cho tam giác ABC có cạnh AC dài 6cm , trên cạnh BC lấy điểm E, sao cho EB = EC. BH là đường cao hạ từ đỉnh B của tam giác ABC và BH = 3cm. EH chia tam giác ABC thành hai phần và diện tích tứ giác ABEH gấp đôi diện tích tam giác CEH.
a/ Tính độ dài đoạn thẳng AH.
SGK Cánh Diều
13 tháng 8 2023 lúc 23:34
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(\alpha \) là số đo của góc nhị diện \(\left[ {A,BC,S} \right]\). Chứng minh rằng tỉ số diện tích của hai tam giác \(ABC\) và \(SBC\) bằng \(\cos \alpha \).
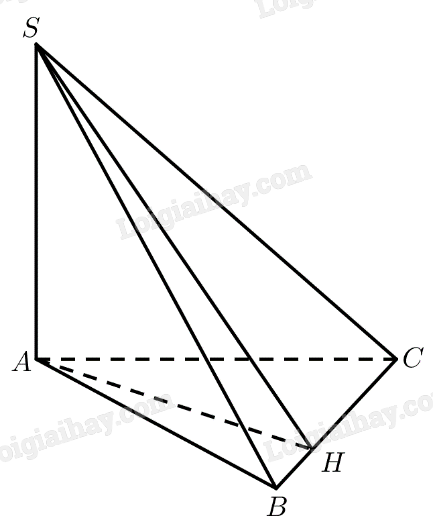
Kẻ \(AH \bot BC\left( {H \in BC} \right)\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)
\( \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {SHA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,S} \right]\)
\( \Rightarrow \widehat {SHA} = \alpha \)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}BC.AH,{S_{\Delta SBC}} = \frac{1}{2}BC.SH\\ \Rightarrow \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{\frac{1}{2}BC.AH}}{{\frac{1}{2}BC.SH}} = \frac{{AH}}{{SH}} = \cos \widehat {SHA} = \cos \alpha \end{array}\)
Đúng 0
Bình luận (0)