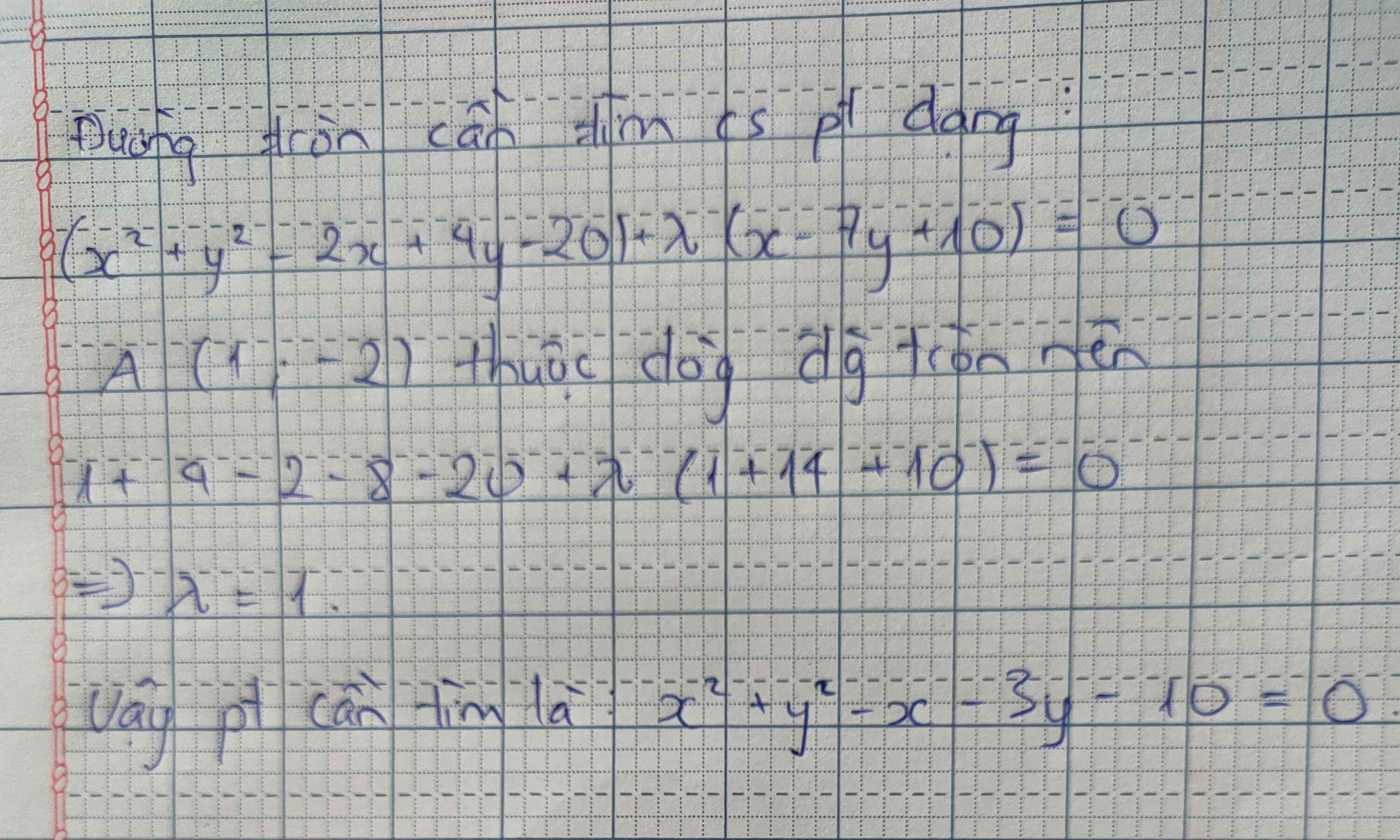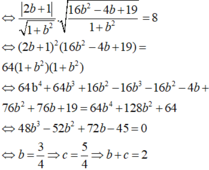Cho đường tròn (C) x2+y2-2x+2y-23=0
Lập phương trình đường thẳng D biết
D đi qua N(7;3) và cắt đường tròn (C) tại hai điểm phân biệt ,EF sao cho NE=3NF

Những câu hỏi liên quan
Trong mặt phẳng với hệ tọa độ cho đường tròn hai đường tròn (C): x2+ y2- 2x -2y +1 0 và (C’) : x2+ y2+ 4x -5 0 cùng đi qua M( 1;0) .Viết phương trình đường thẳng d qua M cắt hai đường tròn lần lượt tại A; B sao cho MA 2 MB. A. 6x+ 6+ y 0 hoặc -6x+ y- 6 0 B. 2x+ 3y + 6 0 hoặc 3x-2y + 3 0 C. 2x+ y- 6 0 hoặc x+ y- 6 0 D. 6x+ y – 6 0 hoặc 6x –y-6 0
Đọc tiếp
Trong mặt phẳng với hệ tọa độ cho đường tròn hai đường tròn (C): x2+ y2- 2x -2y +1= 0 và (C’) : x2+ y2+ 4x -5 = 0 cùng đi qua M( 1;0) .Viết phương trình đường thẳng d qua M cắt hai đường tròn lần lượt tại A; B sao cho MA= 2 MB.
A. 6x+ 6+ y= 0 hoặc -6x+ y- 6= 0
B. 2x+ 3y + 6= 0 hoặc 3x-2y + 3= 0
C. 2x+ y- 6= 0 hoặc x+ y- 6 = 0
D. 6x+ y – 6= 0 hoặc 6x –y-6= 0
Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
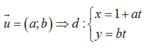
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
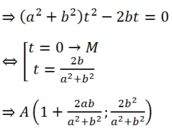
- Nếu d cắt (C2) tại B:
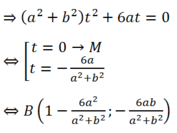
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
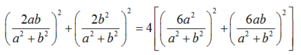
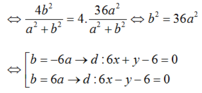
Đúng 0
Bình luận (0)
Bài toán . Cho đường tròn (C) x2+y2-2x+2y-23=0
Lập phương trình đường thẳng D biết
D đi qua M(2;-3)và cắt đường tròn (C) tại hai điểm phân biệt A,B sao cho M là trung điểm của .AB
Đường tròn tâm \(I\left(1;-1\right)\) bán kính \(R=5\)
\(\overrightarrow{IM}=\left(1;-2\right)\Rightarrow IM=\sqrt{5}< R\)
\(\Rightarrow\) M nằm trong đường tròn
Do M là trung điểm AB, theo tính chất đường tròn \(\Rightarrow IM\perp AB\)
\(\Rightarrow\) Đường thẳng d nhận \(\left(1;-2\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-2\left(y+3\right)=0\Leftrightarrow x-2y-8=0\)
Đúng 0
Bình luận (0)
Cho đường tròn (C) : x2+ y2+ 6x -2y + 5= 0 và đường thẳng d đi qua điểm A(- 4;2) , cắt (C) tại hai điểm M; N sao cho A là trung điểm của MN. Phương trình của đường thẳng d là:
A. x-y+ 6 = 0
B.2x+ 3y +2= 0
C.x+ 2y = 0
D. x+ y+2= 0
Đáp án A
Đường tròn (C) có tâm ![]()
Do đó:
![]() ở trong đường tròn.
ở trong đường tròn.
Để A là trung điểm của ![]()
là vectơ pháp tuyến của d nên d có phương trình: -1 (x+ 4) + 1.( y-2) =0
Hay x- y + 6= 0.
Đúng 0
Bình luận (0)
Cho đường tròn (C) có phương trình
x
2
+
y
2
-
6
x
+
2
y
-
5
0
và điểm A(1;0) đường thẳng (d) đi qua A cắt đường tròn theo dây cung MN có độ dài ngắn nhất. Phương trình (d) là A. x+2y+10 B. 2x-y-20 C. 2x-y+20 D. x+2y-10
Đọc tiếp
Cho đường tròn (C) có phương trình x 2 + y 2 - 6 x + 2 y - 5 = 0 và điểm A(1;0) đường thẳng (d) đi qua A cắt đường tròn theo dây cung MN có độ dài ngắn nhất. Phương trình (d) là
A. x+2y+1=0
B. 2x-y-2=0
C. 2x-y+2=0
D. x+2y-1=0
Cho đường tròn (C) : x2 + y2 + 4x - 2y - 11 = 0 và đường thẳng d : 2x - 3y - 5 = 0, a = (-2;1) viết phương trình d’ , C’ lần lượt là ảnh của d và C qua T
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 0 và đường tròn (C) có phương trình
x
2
+
y
2
−
2
x
+
4
y
–
4
0
. Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x 2 + y 2 − 2 x + 4 y – 4 = 0 . Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
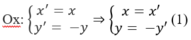
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9
Đúng 0
Bình luận (0)
lập phương trình đường tròn qua A( 1,-2) và qua giao điểm của đường thẳng (d) : x-7y+10=0 với đường tròn x2+y2-2x+4y-20=0
Tham khảo :
mk tham khảo nên ko chắc đúng
\(Đáp án: ( x − 1 2 ) 2 + ( y − 3 2 ) 2 = 25 2 Giải thích các bước giải: Tọa độ giao điểm của (d) và (C) là nghiệm của hệ phương trình { x − 7 y + 10 = 0 x 2 + y 2 − 2 x + 4 y − 20 = 0 ⇔ { x = 7 y − 10 ( 1 ) x 2 + y 2 − 2 x + 4 y − 20 = 0 ( 2 ) Thay (1) vào (2) ta được ( 7 y − 10 ) 2 + y 2 − 2 ( 7 y − 10 ) + 4 y − 20 = 0 ⇔ 49 y 2 − 140 y + 100 + y 2 − 14 y + 20 + 4 y − 20 = 0 ⇔ 50 y 2 − 150 y + 100 = 0 ⇔ y 2 − 3 y + 2 = 0 ⇔ ( y − 2 ) ( y − 1 ) = 0 ⇔ [ y = 2 y = 1 + ) y = 2 ⇒ x = 4 ⇒ B ( 4 ; 2 ) + ) y = 1 ⇒ x = − 3 ⇒ C ( − 3 ; 1 ) Phương trình đường tròn có dạng ( C 1 ) x 2 + y 2 − 2 a x − 2 b y + c = 0 Ta có đường tròn đi qua 3 điểm A ( 1 ; − 2 ) , B ( 4 ; 2 ) , C ( − 3 ; 1 ) A ( 1 ; − 2 ) ∈ ( C 1 ) : 1 2 + ( − 2 ) 2 − 2 a + 4 b + c = 0 ⇔ − 2 a + 4 b + c = − 5 B ( 4 ; 2 ) ∈ ( C 1 ) : 4 2 + 2 2 − 8 a − 4 b + c = 0 ⇔ − 8 a − 4 b + c = − 20 C ( − 3 ; 1 ) ∈ ( C 1 ) : ( − 3 ) 2 + 1 2 + 6 a − 2 b + c = 0 ⇔ 6 a − 2 b + c = − 10 Ta có hệ phương trình ⎧ ⎨ ⎩ − 2 a + 4 b + c = − 5 − 8 a − 4 b + c = − 20 6 a − 2 b + c = − 10 ⇔ ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ a = 1 2 b = 3 2 c = − 10 ⇒ I ( 1 2 ; 3 2 ) , R = √ 1 2 2 + 3 2 2 − ( − 10 ) = 5 √ 2 2 Phương trình đường tròn có dạng ( x − 1 2 ) 2 + ( y − 3 2 ) 2 = 25 2 \)
Đúng 1
Bình luận (2)
Cho đường tròn (C) x2+ y2- 2x + 6y + 6 0 và đường thẳng d: 4x -3y + 5 0. Đường thẳng d’ song song với đường thẳng d và chắn trên (C) một dây cung có độ dài bằng
2
3
có phương trình là: A. 4x- 3y+ 8 0 B.4x-3y- 8 0 hoặc 4x – 3y -18 0 C. 4x- 3y+ 10 0 D. 4x + 3y + 8 0
Đọc tiếp
Cho đường tròn (C) x2+ y2- 2x + 6y + 6= 0 và đường thẳng d: 4x -3y + 5= 0. Đường thẳng d’ song song với đường thẳng d và chắn trên (C) một dây cung có độ dài bằng 2 3 có phương trình là:
A. 4x- 3y+ 8= 0
B.4x-3y- 8= 0 hoặc 4x – 3y -18= 0
C. 4x- 3y+ 10= 0
D. 4x + 3y + 8 = 0
Đáp án B
Đường tròn (C) có tâm I( 1; -3) và R= 2
![]() có phương trình 4x- 3y+ m= 0.
có phương trình 4x- 3y+ m= 0.
Vẽ
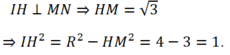
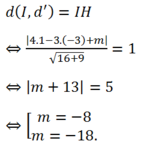

Vậy:
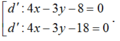
Đúng 1
Bình luận (0)
Trong hệ tọa độ Oxy. Cho đường tròn (C ) có phương trình
x
2
+
y
2
-
4
x
+
2
y
-
15
0
. I là tâm (C ), đường thẳng d qua
M
1
;
-
3
cắt (C ) tại A, B. Biết tam giác IAB có diện tích là 8. Phương trình đường thẳng d là x+by+c0. Tí...
Đọc tiếp
Trong hệ tọa độ Oxy. Cho đường tròn (C ) có phương trình x 2 + y 2 - 4 x + 2 y - 15 = 0 . I là tâm (C ), đường thẳng d qua M 1 ; - 3 cắt (C ) tại A, B. Biết tam giác IAB có diện tích là 8. Phương trình đường thẳng d là x+by+c=0. Tính (b+c)
A. có vô số giá trị
B. 1.
C. 2.
D. 8.