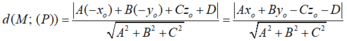Trong không gian Oxyz, cho điểm A(1;1;-1) và mặt phẳng (P): 2x-y+2z+2=0. Biết mặt phẳng đi qua A , vuông góc (P) và tạo với Oy góc lớn nhất có phương trình ax+by+cz-2=0, tính S=2a+b+4c
A. S=5
B. S=3
C. S=7
D. S=6
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : a x + b y + c z - 9 = 0 đi qua hai điểm A 3 ; 2 ; 1 , B - 3 ; 5 ; 2 và vuông góc với mặt phẳng Q : 3 x + y + z + 4 = 0 . Tính tổng S = a + b + c
A. S = -12
B. S = 21
C. S = -4
D. S = 7
Chọn C.
Phương pháp: Lập hệ phương trình tìm a,b,c.
Cách giải: Từ giả thiết ta có hệ:
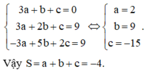
Trong không gian tọa độ Oxyz, nếu mặt phẳng ( P ) : a x + b y + c z + d = 0 chứa trục Oz thì
Trong không gian Oxyz, cho hai mặt phẳn song song (P): Ax + By + Cz + D = 0 và (Q): Ax + By + Cz + D' = 0. M là một điểm di động trên mặt phẳng (P). Khẳng định nào dưới đây có thể sai?
A. Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
B. Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
C. Khoảng cách giữa hai mặt phẳng (P) và (Q) là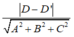 
D. Khoảng cách giữa hai mặt phẳng (P) và (Q) là |D' - D|
Đáp án D
Nếu hai mặt phẳng (P) và (Q) song song với nhau và M thuộc mặt phẳng (P) thì:
+ Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) là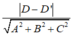 
+ Đặc biệt, khoảng cách giữa hai mặt phẳng (P) và (Q) là |D - D'| khi và chỉ khi:
A 2 + B 2 + C 2 =1
Do đó, mệnh đề D có thể sai.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng (P):x-3y+2z-5=0 Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có dạng ax+by+cz-11=0 Khẳng định nào sau đây là đúng?
A. a+b=c
B. a+b+c = 5
C. a ϵ (b;c)
D. a+b > c
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆ : x - 1 1 = y - 1 1 = z 2 và mặt phẳng P : a x + b y + c z - 3 = 0 . Biết mặt phẳng (P) chứa ∆ và cách O một khoảng lớn nhất. Tổng a + b + c bằng
A. 1
B. 3
C. 2
D. -1
Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng đi qua hai điểm A(1;1;1), B(0;1;2) và khoảng cách từ C(2;-1;1) đến mặt phẳng (P) bằng 3 2 2 . Giả sử phương trình mặt phẳng (P) có dạng ax +by +cz +2 =0. Tính giá trị abc.
A. –2.
B. 2
C. –4
D. 4
Trong không gian với hệ tọa độ Oxyz, mặt phẳng ( P ) : a x + b y + c z + d = 0 , a 2 + b 2 + c 2 > 0 đi qua điểm B(1;0;2) , C(-1;-1;0) và cách A(2;5;3) một khoảng lớn nhất. Khi đó giá trị của biểu thức M = a + c b + d là
A. M = 1
B. M = 3 4
C. M = - 2 7
D. M = - 3 2
Đáp án C.
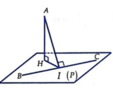
Ta có B C → = - 2 ; - 1 ; - 2 nên phương trình đường thẳng BC là x = 1 - 2 t y = - t ( t ∈ ℝ ) z = 2 - 2 t .
Gọi I là hình chiếu vuông góc của A trên BC, H là hình chiếu vuông góc của A trên mặt phẳng (P) . Khi đó A H = d A ; P ≤ A I và AH đạt giá trị lớn nhất khi H ≡ I . Suy ra mặt phẳng (P) qua I và vuông góc với AI.
Từ I ∈ B C ⇒ I 1 - 2 t ; - t ; 2 - 2 t và A I → = - 1 - 2 t ; - t - 5 ; - 1 - 2 t .
Lại có A I ⊥ B C ⇔ A I → . B C → = 0 ⇔ 2 ( 1 + 2 t ) + ( t + 5 ) + 2 ( 1 + 2 t ) = 0 ⇔ t = - 1 .
Mặt phẳng (P) đi qua I(3;1;4) và nhận VTPT là A I → = 1 ; - 4 ; 1 nên có phương trình tổng quát là: x - 4 y + z - 3 = 0 .
Vậy a = 1 , b = - 4 , c = 1 , d = - 3 → M = 1 + 1 - 4 - 3 = - 2 7 .
Trong không gian Oxyz, cho điểm M(-x0; -y0; z0) và phương trình của mặt phẳng (P): Ax + By + Cz = D = 0. Khoảng cách từ điểm M đến mặt phẳng (P) là:
A. Ax 0 + By 0 + Cz 0 + D A 2 + B 2 + C 2 x
B. Ax 0 + By 0 - Cz 0 - D A 2 + B 2 + C 2
C. - Ax 0 - By 0 + Cz 0 + D A 2 + B 2 + C 2
D. Ax 0 - By 0 - Cz 0 - D A 2 + B 2 + C 2
Đáp án B
Khoảng cách từ điểm M đến mặt phẳng (P) là:
