Viết các số chính phương liên tiếp \(1^2;2^2;3^2;.....;2012^2\) liền nhau ta được số D = 1491625.........4048144
a) Tìm số chữ số của D
b) Tìm số dư trong phép chia D cho 9
Những câu hỏi liên quan
1) Viết liên tiếp các số từ 1-2000 được số A = 123...2000 . Chứng minh A không là số chính phương
1.Chứng minh tích của 4 số tự nhiên liên tiếp không là số chính phương
2.Chứng minh tích của 4 số tự nhiên liên tiếp cộng 1 là số chính phương
3.Chứng minh tích của 4 số tự nhiên chẵn liên tiếp cộng 16 là số chính phương
4.Chứng minh tích của 4 số tự nhiên lẻ liên tiếp cộng 16 là số chính phương
2.
Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x\(\in\) N)
Ta có : x (x+1) (x+2 ) (x+3 ) +1
=( x2 + 3x ) (x2 + 2x + x +2 ) +1
= ( x2 + 3x ) (x2 +3x + 2 ) +1 (*)
Đặt t = x2 + 3x thì (* ) = t ( t+2 ) + 1= t2 + 2t +1 = (t+1)2 = (x2 + 3x + 1 )2
=> x (x+1) (x+2 ) (x+3 ) +1 là số chính phương
hay tích 4 số tự nhiên liên tiếp cộng 1 là số chính phương
Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x
∈
∈ N)
Ta có : x (x+1) (x+2 ) (x+3 ) +1
=( x2 + 3x ) (x2 + 2x + x +2 ) +1
= ( x2 + 3x ) (x2 +3x + 2 ) +1 (*)
Đặt t = x2 + 3x thì (* ) = t ( t+2 ) + 1= t2 + 2t +1 = (t+1)2 = (x2 + 3x + 1 )2
=> x (x+1) (x+2 ) (x+3 ) +1 là số chính phương
hay tích 4 số tự nhiên liên tiếp cộng 1 là số chính phương
Đúng 0
Bình luận (0)
30 tháng 9 2023 lúc 14:23
Bài 1. Chứng minh rằng tổng của 4 số chính phương liên tiếp không thể là một số chính phương.
Bài 2. Chứng minh rằng tổng của 5 số chính phương liên tiếp không thể là một số chính phương.
Bài 3. Cho bốn chữ số 0,2,3,4. Tìm số chính phương có 4 chữ số được tạo bởi cả 4 chữ số trên.
Bài 4. Tìm số nguyên tố p thỏa mãn
a) p 2 + 62 cũng là số nguyên tố.
b) p 2 + 14 và p 2 + 6 cũng là số nguyên tố.
Đọc tiếp
Bài 1. Chứng minh rằng tổng của 4 số chính phương liên tiếp không thể là một số chính phương.
Bài 2. Chứng minh rằng tổng của 5 số chính phương liên tiếp không thể là một số chính phương.
Bài 3. Cho bốn chữ số 0,2,3,4. Tìm số chính phương có 4 chữ số được tạo bởi cả 4 chữ số trên.
Bài 4. Tìm số nguyên tố p thỏa mãn
a) p 2 + 62 cũng là số nguyên tố.
b) p 2 + 14 và p 2 + 6 cũng là số nguyên tố.
cmr
A)tổng các bình phương của 3 số nguyên liên tiếp 0 là số chính phương
B)tổng các bình phương của 4 số nguyên liên tiếp 0 là số chính phương
(n^2 - 1)/3 là tích của hai số tự nhiên liên tiếp cm
a) 2n-1 là số chính phương
b) n là tổng 2 số chính phương liên tiếp giúp
a) Từ giả thiếtta có thể đặt : \(n^2-1=3m\left(m+1\right)\) với m là 1 số nguyên dương
Biến đổi phương trình ta có :
\(\left(2n-1;2n+1\right)=1\) nên dẫn đến :
\(TH1:2n-1=3u^2;2n+1=v^2\)
\(TH2:2n-1=u^2;2n+1=3v^2\)
\(TH1:\)
\(\Rightarrow v^2-3u^2=2\)
\(\Rightarrow v^2=2\left(mod3\right)\)
Còn lại TH2 cho ta \(2n-1\) là số chính phương
b) Ta có :
\(\frac{n^2-1}{3}=k\left(k+1\right)\left(k\in N\right)\)
\(\Leftrightarrow n^2=3k^2+3k+1\)
\(\Leftrightarrow4n^2-1=12k^2+12k+3\)
\(\Leftrightarrow\left(2n-1\right)\left(2n+1\right)=3\left(2k+1\right)^2\)
- Xét 2 trường hợp :
\(TH1:\Rightarrow\hept{\begin{cases}2n-1=3p^2\\2n+1=3q\end{cases}}\)
\(TH2:\Rightarrow\hept{\begin{cases}2n-1=p^2\\2n+1=3q^2\end{cases}}\)
+) TH1 :
Hệ \(PT\Leftrightarrow q^2=3p^2+2=2\left(mod3\right)\) ( loại, vì số chính phương chia 3 dư 0 hoặc 1 )
+) TH2 :
Hệ \(PT\Leftrightarrow p=2a+1\Rightarrow2n=\left(2a+1\right)^2+1\Rightarrow n^2=a^2+\left(a+1\right)^2\) ( dpcm )
1) Tìm tất cả các số nguyên tố để p^4+8^p cũng là số nguyên tố
2)Có tồn tại 2019 số tự nhiên liên tiếp nào mà tổng các bình phương của 2019 số tự nhiên liên tiếp đó là số chính phương không ?
Người ta viết liên tiếp các số 1,2,3...,2015 thành 1 số được sắp xếp theo thứ tự tùy ý. Hỏi số tạo thành theo cách viết trên có thể là số chính phương ko? vì sao?
Người ta viết liên tiếp các số 1,2,3...,2015 thành 1 số được sắp xếp theo thứ tự tùy ý. Hỏi số tạo thành theo cách viết trên có thể là số chính phương ko? vì sao?
Người ta viết liền nhau các số tự nhiên liên tiếp từ 1 đến 135 để tạo thành số tự nhiên A.Số A có phải là số chính phương không? Vì sao?
chứng minh rằng : tổng lập phương các số tự nhiên liên tiếp từ 1 là một số chính phương: 1 mũ 3 + 2 mũ 3 +..... + n mũ3 =(1+2+.....+n) mũ 2
Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
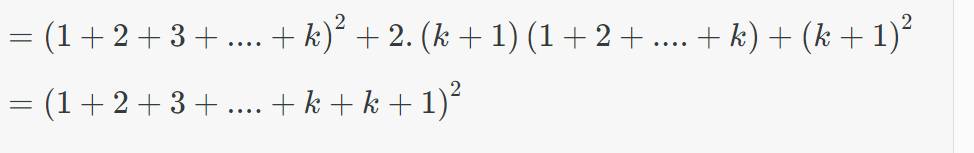
=>ĐPCM
Đúng 0
Bình luận (0)