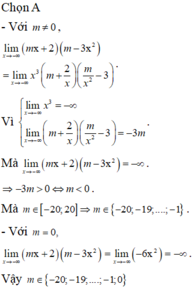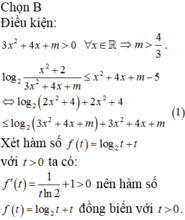Có bao nhiêu giá trị nguyên của m\(\in\)(-20;20) để hàm số \(y=\frac{2x+m}{2x^4+7x^3-\left(3m-4\right)x^2-\left(5m+4\right)x+m^2+2m}\)có tập xác định là R

Những câu hỏi liên quan
Có bao nhiêu giá trị m nguyên thuộc đoạn [-20; 20] để
lim
x
→
-
∞
(
m
x
+
2
)
(
m
-
3
x
2
)
-
∞
A. 21 B. 22 C. 20 D. 41
Đọc tiếp
Có bao nhiêu giá trị m nguyên thuộc đoạn [-20; 20] để lim x → - ∞ ( m x + 2 ) ( m - 3 x 2 ) = - ∞
A. 21
B. 22
C. 20
D. 41
Có bao nhiêu giá trị nguyên dương của
m
20
để bất phương trình
log
2
x
2
+
2
3
x
2
+
4
x...
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của m < 20 để bất phương trình log 2 x 2 + 2 3 x 2 + 4 x + m ≤ x 2 + 4 x + m - 5 có nghiệm ∀ x ∈ R .
A. 15.
B.12
C.14
D.13
Có bao nhiêu giá trị nguyên dương của
m
20
để bất phương trình
log
2
x
2
+
2
3
x
2
+
4
x
+
m
≤
x
2
+...
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của m < 20 để bất phương trình log 2 x 2 + 2 3 x 2 + 4 x + m ≤ x 2 + 4 x + m - 5 có nghiệm ∀ x ∈ ℝ .
A. 15
B. 12
C. 14
D. 13
Có tất cả bao nhiêu giá trị nguyên của m để phương trình
m
x
2
+
20
c
o
s
x
20
có đúng hai nghiệm thực phân biệt thuộc đoạn
0
;
π
2
A. 1 B. 2 C. 3 D. 0
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của m để phương trình m x 2 + 20 c o s x = 20 có đúng hai nghiệm thực phân biệt thuộc đoạn 0 ; π 2
A. 1
B. 2
C. 3
D. 0
Có tất cả bao nhiêu giá trị nguyên của m để phương trình
m
x
2
+
20
cos
x
20
có đúng hai nghiệm thực phân biệt thuộc đoạn
0
;
π
2
A. 1. B. 2. C. 3. D. 0.
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của m để phương trình m x 2 + 20 cos x = 20 có đúng hai nghiệm thực phân biệt thuộc đoạn 0 ; π 2
A. 1.
B. 2.
C. 3.
D. 0.
Có tất cả bao nhiêu giá trị nguyên của m để phương trình m x 3 + 20 cos x = 20 có đúng hai nghiệm thực phân biệt thuộc đoạn 0 ; π 2 .
A. 1
B. 2
C. 3
D. 0
Đáp án A
Với mọi m phương trình luôn có nghiệm x = 0
Đúng 0
Bình luận (0)
Câu 1: Gọi M là tập hợp tất cả các giá trị nguyên của tham số m để phương trình -x^2+left(2m-3right)x-m^2+m+200 có hai nhgieemj trái dấu. Tổng tất cả các phần tử của M bằngA. 5 B. 4 C. 10 D. 15Câu 2: Có tất cả bao nhiêu giá trị nguyên của tham số m nhỏ hơn 2022 để bất phương trình x^2-8x+m+20ge0 nghiệm đúng với mọi x ϵ [5; 10]?A. 2027 B. 2028 C. 2062 D. 2063
Đọc tiếp
Câu 1: Gọi M là tập hợp tất cả các giá trị nguyên của tham số m để phương trình \(-x^2+\left(2m-3\right)x-m^2+m+20=0\) có hai nhgieemj trái dấu. Tổng tất cả các phần tử của M bằng
A. 5 B. 4 C. 10 D. 15
Câu 2: Có tất cả bao nhiêu giá trị nguyên của tham số m nhỏ hơn 2022 để bất phương trình \(x^2-8x+m+20\ge0\) nghiệm đúng với mọi x ϵ [5; 10]?
A. 2027 B. 2028 C. 2062 D. 2063
Có bao nhiêu cặp số nguyên (x;y) thỏa mãn
giá trị tuyệt đói của x+ giá trị tuyệt đối của y =20
giá trị tuyệt đối của x+ giá trị tuyệt đối của y <20
Cho phương trình \(5^x+m=log_5\left(x-m\right)\) với m là tham số. Có bao nhiêu giá trị nguyên của \(m\in\left(-20;20\right)\) để phương trình đã cho có nghiệm
https://video.vietjack.com/upload2/quiz_source1/2020/01/100-bai-trac-nghiem-ham-so-mu-va-logarit-co-loi-giai-chi-tiet-3-1-1579254891.PNG
bạn tham khảo nha
Đúng 2
Bình luận (0)
Cho `A={x in R` | `|x-m|=25} ; B={x in R` | `|x| >= 2020}` . Có bao nhiêu giá trị nguyên m thì \(A\cap B=\varnothing\)
\(\left|x-m\right|=25\Leftrightarrow\left[{}\begin{matrix}x=m+25\\x=m-25\end{matrix}\right.\)
\(\left|x\right|\ge2020\Leftrightarrow\left[{}\begin{matrix}x\ge2020\\x\le-2020\end{matrix}\right.\)
+) \(x=m+25\)
Để \(A\cap B=\varnothing\) \(\Leftrightarrow\left\{{}\begin{matrix}m+25>-2020\\m+25< 2020\end{matrix}\right.\)\(\Leftrightarrow-2045< m< 1995\)
+) \(x=m-25\)
Để \(A\cap B=\varnothing\) \(\Leftrightarrow\left\{{}\begin{matrix}m-25>-2020\\m-25< 2020\end{matrix}\right.\)\(\Leftrightarrow-1995< m< 2045\)
Đúng 1
Bình luận (3)