a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:

$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$

Với I là tâm đường tròn, A là điểm trên đường tròn.

Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$

Thay vào công thức ta được:

$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$

Vậy bán kính của đường tròn là $\sqrt{34}$.

Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:

$(x-2)^2 + (y-3)^2 = 34$

b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.

Ta có phương trình đường tròn chính giữa:

$(x-1)^2 + (y+5)^2 = 2^2$

Đạo hàm hai vế theo x:

$2(x-1) + 2(y+5)y' = 0$

Suy ra:

$y' = -\frac{x-1}{y+5}$

Tại điểm M(x,y) trên đường tròn, ta có:

$(x-1)^2 + (y+5)^2 = 2^2$

Đạo hàm hai vế theo x:

$2(x-1) + 2(y+5)y' = 0$

Suy ra:

$y' = -\frac{x-1}{y+5}$

Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:

$y - y_M = y'(x-x_M)$

Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:

$y + 5 = \frac{-(x-1)}{y+5}(x-1)$

Simplifying:

$x(y+5) + y(x-1) = 6$

Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến

Em ghi lại pt đường tròn nhé, bị lỗi rồi

Đáp án B

Đường tròn (C) có tâm I( 2;2) và bán kính R= 3.

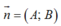 là vectơ pháp tuyến của tiếp tuyến d :

d : A(x- 5) + B( y+1) =0  

Do d là tiếp tuyến của (C) nên:

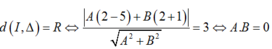
+ Nếu A= 0, chọn B = 1 ta được d : y+1= 0

+ Nếu B= 0, chọn A= 1 ta được d : x- 5= 0

Đường tròn (C): x 2 + y 2 + 4 x − 2 y − 4 = 0  có tâm I(-2; 1) và bán kính R = 3.

Ta có : I M = 1 + 2 2 + 2 − 1 2 = 10 > 3  nên M nằm ngoài đường tròn.

Qua M kẻ được hai tiếp tuyến đến đường tròn.

ĐÁP ÁN C