Cho hình vuông ABCD biết A(0;2) , phương trình (BD) : x-3y+1=0
Tìm 3 đỉnh còn lại của hình vuông
Cho hình vuông ABCD và hình tròn tâm 0 như hình vẽ:a,cho biết diện tích hình vuông bằng 25cm2.Tính diện tích hình tròng
b,cho biết diện tích hính vuông bằng 12cm2.Tính diện tích phần gạch chéo?
`a)` Vì `5xx5=25` nên cạnh hình vuông bằng `5 cm`
Bán kính hình tròn là: `5:2=2,5(cm)`
Diện tích hình tròn là: `2,5xx2,5xx3,14=19,625(cm^2)`
`b)` Vì `2\sqrt{3}xx2\sqrt{3}=12` nên cạnh hình vuông bằng `2\sqrt{2} cm`
Bán kính hình tròn là: `2\sqrt{3}:2=\sqrt{3})(cm)`
Diện tích hình tròn là: `\sqrt{3}xx\sqrt{3}xx3,14=9,42(cm^2)`
Diện tích phần gạch chéo là: `12-9,42=2,58(cm^2)`
Chỗ dòng đầu của câu `b` sửa cạnh hình vuông bằng `2\sqrt{3}cm` nhé!
bài này dễ nhưng mong bạn có thể vẽ đẹp hơn nhé, nhìn chẳng ra hình tròn cũng chẳng ra hình vuông:)))))))
Cho hình vuông ABCD biết A(0;2), BC: x -2y-1=0 và điểm C có hoành độ dương. Tìm tọa độ tâm N của hình vuông ABCD.
Do ABCD là hình vuông \(\Rightarrow AB=d\left(A;BC\right)=\dfrac{\left|0-2.2-1\right|}{\sqrt{1^2+\left(-2\right)^2}}=\sqrt{5}\)
\(\Rightarrow AC=AB\sqrt{2}=\sqrt{10}\)
Do C thuộc BC \(\Rightarrow C\left(2c+1;c\right)\) \(\Rightarrow\overrightarrow{AC}=\left(2c+1;c-2\right)\)
\(\Rightarrow AC^2=\left(2c+1\right)^2+\left(c-2\right)^2=10\)
\(\Leftrightarrow5c^2-5=0\Rightarrow\left[{}\begin{matrix}c=1\\c=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}C\left(3;1\right)\\C\left(-1;-1\right)\end{matrix}\right.\)
Do C có hoành độ dương \(\Rightarrow C\left(3;1\right)\)
N là trung điểm AC \(\Rightarrow N\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
Cho hình vuông ABCD và hình tròn tâm 0 như hình vẽ:
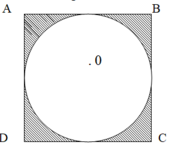
a, Cho biết diện tích hình vuông bằng 25 c m 2 .
Tính diện tích hình tròn?
Cho hình vuông ABCD và hình tròn tâm 0 như hình vẽ :
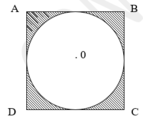
a, Cho biết diện tích hình vuông bằng 25 c m 2 .
Tính diện tích hình tròn?
b, Cho biết diện tích hình vuông bằng 12 c m 2
Tính diện tích phần gạch chéo?
Cho hình vuông ABCD và hình tròn tâm 0 như hình vẽ :
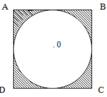
a. Cho biết diện tích hình vuông bằng 25 c m 2 .Tính diện tích hình tròn?
b. Cho biết diện tích hình vuông bằng 12 c m 2 . Tính diện tích phần gạch chéo?
a. Từ hình vẽ, ta thấy cạnh của hình vuông B bằng đường kính của hình tròn - do đó ta có:
|
( R x 2 ) x ( R x 2 ) = 25
R x 2 x R x 2 = 25
R x R x 4 = 25
R x R = 25 : 4 = 6,25
Vậy diện tích hình tròn là: 6,25 x 3,14 = 19,625 ( c m 2 )
b, Vì ( R x 2 ) x ( R x 2 ) = 12
R x R x 4 = 12
R x R = 12 : 4 = 3
Vậy diện tích phần gạch chéo là: 3 x 3,14 : 4 = 0,645 ( c m 2 )
Đáp số: 19,625 c m 2
0,645 c m 2
a)19,625
B) không biết
a. Từ hình vẽ, ta thấy cạnh của hình vuông B bằng đường kính của hình tròn - do đó ta có:
|
( R x 2 ) x ( R x 2 ) = 25
R x 2 x R x 2 = 25
R x R x 4 = 25
R x R = 25 : 4 = 6,25
Vậy diện tích hình tròn là: 6,25 x 3,14 = 19,625 ( c m 2 )
b, Vì ( R x 2 ) x ( R x 2 ) = 12
R x R x 4 = 12
R x R = 12 : 4 = 3
Vậy diện tích phần gạch chéo là: 3 x 3,14 : 4 = 0,645 ( c m 2 )
Đáp số: 19,625 c m 2
0,645 c m 2
nhớ tim nhé
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại A và B, Kẻ \(SA\) vuông góc với \(mp\left(ABCD\right)\). Biết rằng \(AB=BC=a\), \(AD=2a\) góc giữa \(SB\) và \(mp\left(ABCD\right)\) bằng \(45^0\)
a) Chứng minh rằng BC vuông góc với SB, và \(mp\left(SCD\right)\perp mp\left(SAC\right)\)
b) Gọi \(mp\left(\alpha\right)\) là mặt phẳng đi qua A và vuông góc với SC. Xác định thiết diện của hình chóp \(S.ABCD\) và \(mp\left(\alpha\right)\). Tính diện tích của thiết diện đó theo \(a\).
P/s: Em xin nhờ quý thầy cô giáo và các bạn yêu toán trên toàn quốc giúp em ý b với ạ
Em cám ơn nhiều lắm ạ!
trong mặt phẳng với hệ tọa độ Oxy, cho hình thang vuông ABCD ( vuông tại A và B ) . Gọi M(-3,-3) N lần lược là trung điểm của AD và AB . Xác định tọa độ các đỉnh của hình thang vuông ABCD , biết phương trình các đường thẳng BD: 7x+3y+2=0, CN: x-3y=0, CN: x-y=0và đường thẳng AB đi qua điểm e (-3;1)
Đường CN có pt là x-3y=0 hay x-y=0 vậy bạn?
Cho hình vuông ABCD và hình tròn tâm 0 như hình vẽ:
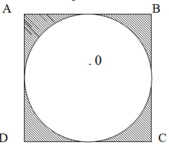
b, Cho biết diện tích hình vuông bằng 12 c m 2 .
Tính diện tích phần gạch chéo?
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết AB=2a, AD=DC=a. Cạnh bên SA vuông góc với đáy và \(SA=a\sqrt{2}\). CHọn khẳng định sai?
A: \(\widehat{\left(SBC\right);\left(ABCD\right)}=45^0\)
B: \(\widehat{\left(SDC\right);\left(BCD\right)}=60^0\)
C: Giao tuyến của (SAB) với (SCD) song song AB
D: \(\left(SBC\right)\perp\left(SAC\right)\)
B là khẳng định sai
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD=\left(SCD\right)\cap\left(BCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SDC) và (BCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'\)
cho hình thang ABCD vuông tại A biết CD=2AB=2AD. Gọi I là giao điểm BC, DH vuông AC.Chứng minh HDI= 450