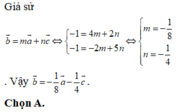Cho hai vectơ vecto a =(-1;1). Vecto b=(2;0) góc giữa hai vecto a và vecto b là

Những câu hỏi liên quan
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?a, Hai vecto cùng hướng thì cùng phương.b, Hai vecto b→ và kb→ cùng phương.c, Hai vecto a→ và (-2)a→ cùng hướng.d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
Đọc tiếp
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?
a, Hai vecto cùng hướng thì cùng phương.
b, Hai vecto b→ và kb→ cùng phương.
c, Hai vecto a→ và (-2)a→ cùng hướng.
d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
TL: A, B, D: Đúng; C: Sai
Cho các vectơ
a
→
(4; -2),
b
→
(-1;-1),
c
→
(2;5). Phân tích vecto
b
→
theo hai vecto
a
→
và
c
→
ta được: A. B. C. D.
Đọc tiếp
Cho các vectơ a → = (4; -2), b → = (-1;-1), c → = (2;5). Phân tích vecto b → theo hai vecto a → và c → ta được:
A. 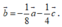
B. 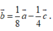
C. 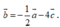
D. 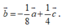
Cho các vectơ
a
→
4
;
-
2
,
b
→
-
1
;
-
1
,
c
→
2
;
5
. P...
Đọc tiếp
Cho các vectơ a → = 4 ; - 2 , b → = - 1 ; - 1 , c → = 2 ; 5 . Phân tích vecto b → theo hai vectơ a → và c → ta được:
![]()
![]()
![]()
![]()
cho vectơ u=vectơ a +3 vecto b vuông góc với vectơ v=7 vecto a-5 vecto b và vecto x= vecto a-4 vecto b vuông góc với vecto y=7 vecto a-2 vecto b. khi đó góc giữa 2 vecto a và b bằng bao nhiêu
Cho tam giác ABC có trọng tâm G Gọi I và J lần lượt là hai điểm thỏa mãn vectơ IB = vectơ BA , vecto JA= -2/3 vecto JC .
a)CM: vecto IJ=2/5 vecto AC - 2 vecto AB
b) tính vecto IG theo vecto AB và vecto AC
Cho tam giác ABC có trọng tâm G Gọi I và J lần lượt là hai điểm thỏa mãn vectơ IB = vectơ BA , vecto JA= -2/3 vecto JC . CM: vecto IJ=2/5 vecto AC - 2 vecto AB
Ta có \(\overrightarrow{IB}=\overrightarrow{BA}\Rightarrow\hept{\begin{cases}I\in AB\\\overrightarrow{AI}=2\overrightarrow{AB}\end{cases}}\). Tương tự \(\hept{\begin{cases}J\in\left[AC\right]\\\overrightarrow{AJ}=\frac{AJ}{AC}\overrightarrow{AC}=\frac{2}{5}\overrightarrow{AC}\end{cases}}\)
Do đó \(\overrightarrow{IJ}=\overrightarrow{AJ}-\overrightarrow{AI}=\frac{2}{5}\overrightarrow{AC}-2\overrightarrow{AB}\)(đpcm).
Đúng 0
Bình luận (0)
giải giúp t câu này nha : tính vecto IG theo vecto AB và vecto AC (các b vẽ hình ra hộ t nhé)
Đúng 0
Bình luận (0)
cho tam giác ABC có trọng tâm G và N là điểm thỏa mãn vectơ AN = vectơ GC. Hãy xác định vị trí điểm N.
Đúng 0
Bình luận (0)
1Vẽ tam giác ABC và tam giác định tổng các vectơ sau : vecto AB + vecto CB và vecto AC + vecto BC.
2 Cho hình bình hành ABCD tâm O . Hãy vẽ vectơ AB dưới dạng tổng của hai vectơ mà các đầu mút lấy I trong 5 điểm A , B,C,D,O.
3 Chứng minh rằng vectơ AB = vectơ CD , vectơ AC = vectơ BD với 4 điểm tùy ý ABCD
Chứng minh rằng
a) Vecto AD - vectơ BC + vectơ AB = vectơ CD - vectơ BE
b) Vecto AB - vecto DC - vecto FE = vecto CF - vecto DA + vecto EB
Chưa đủ dữ kiện đề bài để chứng minh đẳng thức. Bạn xem lại đề.
Đúng 0
Bình luận (0)
Cho hai vectơ
a
→
và
b
→
khác vecto không và thảo mãn
u
→
a
→
+
b
→
vuông góc với vecto
v
→
2
a
→
-
3
b
→
và
m...
Đọc tiếp
Cho hai vectơ a → và b → khác vecto không và thảo mãn u → = a → + b → vuông góc với vecto v → = 2 a → - 3 b → và m → = 5 a → - 3 b → vuông góc với n → = - 2 a → + 7 b → . Tính góc tạo bởi hai vecto a → và b →
A. 60 °
B. 45 °
C. 90 °
D. 30 °