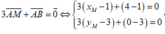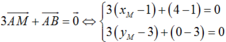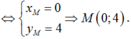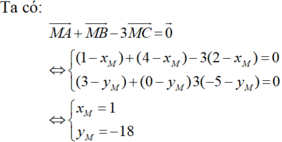Trong mặt phẳng Oxy cho điểm A(0;3) ; B(3;1), tọa độ điểm M thỏa mãn \(\overrightarrow{MA}\) = -2\(\overrightarrow{AB}\)

Những câu hỏi liên quan
Bài 3. Trong mặt phẳng Oxy cho các điểm A(0,−2), B(1,0), C(5,−1) và D(−2,3).
a) Dựng các điểm A, B, C, D trên mặt phẳng tọa độ Oxy.
cho minh hoi dung cai diem laf no keu minh lam gif he
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa
3
A
M
→
+
A
B
→
0
→
là A.M( 4; 0) B.M( 0; 4) C.M( 5;3) D.M( 2; 8)
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa 3 A M → + A B → = 0 → là
A.M( 4; 0)
B.M( 0; 4)
C.M( 5;3)
D.M( 2; 8)
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa
3
A
M
→
+
A
B
→
0
→
là A. M(4; 0) B. M(0; 4) C. M(5;3) D. M(2; 8)
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa 3 A M → + A B → = 0 → là
A. M(4; 0)
B. M(0; 4)
C. M(5;3)
D. M(2; 8)
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho
M
A
→
+
M
B
→
+
M
C
→
0
→
.
A. M (-2; 0) B. M(2; 0) C. M(- 4; 0) D. M(- 5; 0)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho M A → + M B → + M C → = 0 → .
A. M (-2; 0)
B. M(2; 0)
C. M(- 4; 0)
D. M(- 5; 0)
Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho hai điểm F1(-4; 0) và F2(4;0) và điểm A(0; 3). Điểm M thuộc E nào sau đây thỏa MF1 3MF2.
Đọc tiếp
Trong mặt phẳng Oxy, cho hai điểm F1(-4; 0) và F2(4;0) và điểm A(0; 3). Điểm M thuộc E nào sau đây thỏa MF1= 3MF2.
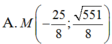
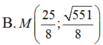
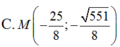
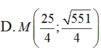
Đáp án B
- Giả sử:
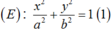
Theo giả thiết thì : c = 4 nên a2- b2= 16 (2)
(E) qua A suy ra :
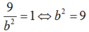
thay vào (2) ta có:
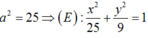
M thuộc (E)
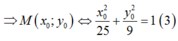
Theo tính chất của (E) ta có bán kính qua tiêu
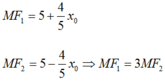
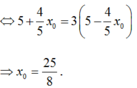
Thay vào ta có:
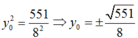
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm A(3; 4) và hàm số y = 4/3 x .
a) Điểm A có thuộc đồ thị của hàm số y = 4/3 x hay không? Vì sao?
b) Vẽ đồ thị của hàm số y = 4/3 x .
c) Xác định các điểm H(3; 0), P(6; 0), Q(0; 4) trên mặt phẳng tọa độ Oxy ở trên.
d) Chứng minh AO = AP
a: \(y=\dfrac{4}{3}\cdot3=4\)
=>A có thuộc đồ thị
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm A(3; 4) và hàm số y = 4/3 x .
a) Điểm A có thuộc đồ thị của hàm số y = 4/3 x hay không? Vì sao?
b) Vẽ đồ thị của hàm số y = 4/3 x .
c) Xác định các điểm H(3; 0), P(6; 0), Q(0; 4) trên mặt phẳng tọa độ Oxy ở trên.
d) Tam giác AOP là tam giác gì? Vì sao? Tính diện tích của tam giác AOP.
a: y=4/3x3=4
=>A có thuộc đồ thị y=4/3x
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxy cho mặt phẳng
P
:
2
x
-
y
-
z
+
1
0
và hai điểm
A
2
;
1
;
1
,
B
3
;
3
;
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxy cho mặt phẳng P : 2 x - y - z + 1 = 0 và hai điểm A 2 ; 1 ; 1 , B 3 ; 3 ; 2 . Điểm M a ; b ; c với b > 0 nằm trong mặt phẳng (P) sao cho O M ⊥ A B và M A = 26 . Giá trị của tổng a + b + c bằng.
A. 1
B. 3
C. -2
D. 5
Chọn C.
Phương pháp: Dựa vào dữ kiện bài toán để xác định tọa độ điểm M.
Cách giải: Ta có:

Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ; B( 4; 0) ; C(2; -5). Tọa độ điểm M thỏa mãn
M
A
→
+
M
B
→
-
3
M
C
→
0
→
là A. M(1; -18). B. M(1 ;18). C. M(18; -1). D. M(-18; -1).
Đọc tiếp
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ; B( 4; 0) ; C(2; -5). Tọa độ điểm M thỏa mãn M A → + M B → - 3 M C → = 0 → là
A. M(1; -18).
B. M(1 ;18).
C. M(18; -1).
D. M(-18; -1).
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ;; B( 4; 0) ; C( 2; -5). Tọa độ điểm M thỏa mãn
M
A
→
+
M
B
→
-
3
M
C
→
0
→
là A.M( 1; -18) B.M( 1 ;18) C.M( 18; -1 D.M(...
Đọc tiếp
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ;; B( 4; 0) ; C( 2; -5). Tọa độ điểm M thỏa mãn M A → + M B → - 3 M C → = 0 → là
A.M( 1; -18)
B.M( 1 ;18)
C.M( 18; -1
D.M( -18; -1)