Gọi d là đường thẳng đi qua A(1;0) và có hệ số góc m. Tìm tất cả giá trị thực của tham số m để d cắt đồ thị hàm số y=\(\dfrac{x+2}{x-1}\)(C) tại hai điểm phân biệt thuộc 2 nhánh của đồ thị
A. m<0 B. 0<m\(\ne\)1 C. m\(\ne\)0 D. m>0
Những câu hỏi liên quan
Cho đường thẳng
∆
:
x
+
1
2
y
3
z
+
1
-
1
và hai...
Đọc tiếp
Cho đường thẳng ∆ : x + 1 2 = y 3 = z + 1 - 1 và hai điểm A(1;2;-1), B(3;-1;-5) . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Phương trình của d là:
A. x - 3 2 = y 2 = z + 5 - 1
B. x - 1 = y + 2 3 = z 4
C. x + 2 3 = y 1 = z - 1 - 1
D. x - 1 1 = y - 2 2 = z + 1 - 1
Đáp án là D.
Ta có:
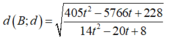
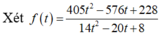
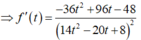
Đường thẳng d đi qua A(1;2;-1) và có VTCP
Đúng 0
Bình luận (0)
Cho đường thẳng
Δ
:
x
+
1
2
y
3
x
+
1
−
1
và hai điểm
A
1
;
2
;
−
1
,
...
Đọc tiếp
Cho đường thẳng Δ : x + 1 2 = y 3 = x + 1 − 1 và hai điểm A 1 ; 2 ; − 1 , B 3 ; − 1 ; − 5 . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Phương trình của d là:
A. x − 3 2 = y 2 = z + 5 − 1
B. x − 1 = y + 2 3 = z 4
C. x + 2 3 = y 1 = z − 1 − 1
D. x − 1 1 = y − 2 2 = z + 1 − 1
Đáp án là D.
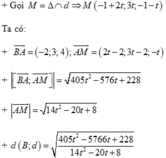
Xét f t = 405 t 2 − 576 t + 228 14 t 2 − 20 t + 8 ⇒ f ' t = − 36 t 2 + 96 t − 48 14 t 2 − 20 t + 8 2
f ' t = 0 ⇔ t = 2 t = 2 3 . Vậy max f t = f 2 ⇒ t = 2
+ Đường thẳng d đi qua A 1 ; 2 ; − 1 và có VTCP A M → = 2 ; 4 ; − 2 = 2 1 ; 2 ; − 1
Đúng 0
Bình luận (0)
Bài 1. Cho đường thẳng d, 2 điểm A và B nằm cùng ở một mặt phẳng có bờ là đường thẳng d ( A,B không thuộc d). Gọi C và D thứ tự là điểm đối xứng của A,B qua đường thẳng d.a. Chứng minh tứ giác ABCD là hình thang cânb. Gọi E là giao điểm của BC và đường thẳng d, F thuộc đường thẳng d, F khác E. Chứng minh BF+FCBE+EAc. 1 người đi từ A đến d rồi lại về B. Hỏi đi qua đường nào là ngắn nhất
Đọc tiếp
Bài 1. Cho đường thẳng d, 2 điểm A và B nằm cùng ở một mặt phẳng có bờ là đường thẳng d ( A,B không thuộc d). Gọi C và D thứ tự là điểm đối xứng của A,B qua đường thẳng d.
a. Chứng minh tứ giác ABCD là hình thang cân
b. Gọi E là giao điểm của BC và đường thẳng d, F thuộc đường thẳng d, F khác E. Chứng minh BF+FC>BE+EA
c. 1 người đi từ A đến d rồi lại về B. Hỏi đi qua đường nào là ngắn nhất
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
Δ
:
x
+
1
2
y
3
z
+
1
−
1
và hai điểm
A
1
;
2
;
−...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ : x + 1 2 = y 3 = z + 1 − 1 và hai điểm A 1 ; 2 ; − 1 , B 3 ; − 1 ; − 5 . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Khi đó, gọi M a ; b ; c là giao điểm của d với đường thẳng Δ . Giá trị P = a + b + c bằng
A. -2
B. 4
C. 2
D. 6
- Tính khoảng cách từ B đến d theo t và tìm GTLN của khoảng cách.
- Tìm t và suy ra tọa độ của M.
Cách giải:
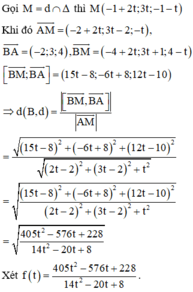
Sử dụng MTCT (chức năng TABLE với bước START nhập -5, bước END nhập 5 và bước STEP nhập 1 ta sẽ được kết quả GTLN f t = 29 tại t = 2)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
∆
:
x
+
1
2
y
3
z
+
1
-
1
và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 1 2 = y 3 = z + 1 - 1 và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là:
A . x - 3 2 = y 2 = z + 5 - 1
B . x - 1 = y + 2 3 = z 4
C . x + 2 3 = y 1 = z - 1 - 1
D. Tất cả sai
Chọn D
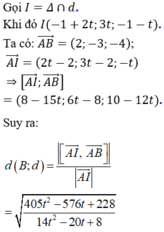
Xét hàm số:
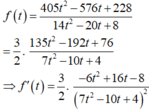
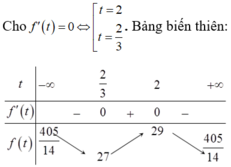
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra 
. Chọn một vectơ chỉ phương của đường thẳng d là 
Vậy phương trình đường thẳng 
Đúng 0
Bình luận (0)
cho đường tròn (O) đường kính AB. Đường thẳng a tiếp xúc với (O) tại A. Gọi M đi đông trên (O). Tiếp tuyến của (O) tại M cắt a tại C. Gọi I là tâm đường tròn tiếp xúc với a tại C đi qua M. Kẻ CD là đường kính (I). GỌi K là giao điểm của OC với (I). CMR
a, K là trung điểm của OC
b, ĐƯờng thẳng qua D vuông góc với BC luôn qua 1 điểm cố định
a) Ta có CA,CM là các tiếp tuyến từ C tới đường tròn (O) => OC là phân giác của ^AOM => ^MOC = ^AOC
Ta thấy ^CMD là góc chắn nửa đường tròn (I) => ^CMD = 900 => ^CMD + ^CMO = 1800
=> 3 điểm D,M,O thẳng hàng => ^DOC = ^MOC. Mà ^MOC = ^AOC nên ^DOC = ^AOC
Hai đường tròn (O),(I) cùng tiếp xúc với a => CD // AB (Cùng vuông góc với a)
Do đó ^AOC = ^DCO (So le trong) => ^DOC = ^DCO => \(\Delta\)ODC cân tại D
Lại có DK vuông góc OC tại K (Vì ^DKC chắn nửa đường tròn) => K là trung điểm OC (đpcm).
b) Gọi đường thẳng qua D vuông góc với BC cắt BC,AB lần lượt tại H,S.
Dễ thấy điểm H nằm trên đường tròn (I) => ^HMO = ^HCD = ^HBO (Do CD // AB)
=> Tứ giác HOBM nội tiếp => ^OHB = ^OMB => 900 - ^OHB = 900 - ^OMB
=> ^OHS = 900 - ^ABM = ^MAB = ^ACO (Cùng phụ ^CAM) (1)
Ta lại có ^SHK = ^DCK = ^SOK (Vì AB // CD) => Tứ giác KHOS nội tiếp => ^OHS = ^OKS (2)
Từ (1) và (2) suy ra ^ACO = ^OKS => KS // AC. Xét \(\Delta\)CAO có:
K là trung điểm cạnh OC (cmt), KS // AC (cmt), S thuộc OA => S là trung điểm cạnh OA
Do 2 điểm O,A cố định nên S cũng cố định. Mà đường thẳng qua D vuông góc BC cắt OA tại S
Nên ta có ĐPCM.
Đúng 0
Bình luận (0)
Cho A(-1;2) và d1: 2x-y+1=0, vecto v=(4;-3). Gọi d2 là đường thẳng đi qua A và vuông góc với d1. Viết phương trình đường thẳng d’ là ảnh của d2 qua phép tịnh tiến
\(d_2\) vuông góc \(d_1\) nên nhận (1;2) là 1 vtpt
d' là ảnh của \(d_2\) qua phép tịnh tiến \(\Rightarrow d'\) cùng phương \(d_2\Rightarrow d'\) cũng nhận (1;2) là 1 vtpt, pt d' có dạng:
\(x+2y+c=0\) (1)
Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)
\(\left\{{}\begin{matrix}x'=-1+4=3\\y'=2+\left(-3\right)=-1\end{matrix}\right.\) \(\Rightarrow A'\left(3;-1\right)\)
Thế vào (1):
\(3+2.\left(-1\right)+c=0\Rightarrow c=-1\)
Vậy pt d' là: \(x+2y-1=0\)
Đúng 2
Bình luận (0)
Vẽ đồ thị (P) của hàm số y=\(-2x^2\) trên mặt phẳng tọa độ Oxy
1. Gọi (d) là đường thẳng đi qua điểm A (-2;-1) và có hệ số góc k
a. Viết phương trình đường thẳng (d)
b. Tìm k để (d) đi qua B nằm trên (P) biết hoành độ của B là 1.
a)Gọi pt đường thẳng d là: \(y=ax+b\left(a\ne0\right)\)
Vì d có hệ số góc là k \(\Rightarrow a=k\)
Vì (d) đi qua điểm \(A\left(-2;-1\right)\Rightarrow-1=-2k+b\Rightarrow b=\dfrac{1}{2k}\)
\(\Rightarrow\left(d\right):y=kx+\dfrac{1}{2k}\)
b) Vì điểm \(B\in\left(P\right)\Rightarrow y_B=-2x_B^2=-2\Rightarrow B\left(1;-2\right)\)
\(\Rightarrow-2=k+\dfrac{1}{2k}\Leftrightarrow-2=\dfrac{2k^2+1}{2k}\Rightarrow-4k=2k^2+1\)
\(\Rightarrow2k^2+4k+1=0\)
\(\Delta=4^2-4.2=8\)
\(\Rightarrow\left[{}\begin{matrix}k=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-4-\sqrt{8}}{4}=\dfrac{-2-\sqrt{2}}{2}\\k=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-4+\sqrt{8}}{4}=\dfrac{-2+\sqrt{2}}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
vẽ theo mô tả
cho 3 điểm ABC ko thẳng hàng
vẽ đường thẳng m đi qua 2 điểm A,B
vẽ đường thẳng n đi qua 2 điểm A,C
vẽ điểm D sao cho điểm C nằm giữa hai điểm A và điểm D
qua C , vẽ đường thẳng p song song với đường thẳng AB
gọi E là giao điểm của đường thẳng p và đường thẳng đi qua hai điểm D,B
gọi (d) là đường thẳng y=(2k-1)x+k-2 với k là tham số
a) Định k để (d) đi qua điểm (1;6)
b) Định k để (d) song song với đường thẳng 2x+3y-5 =0
c) Định k để (d) vuông góc với dường thẳng x+2y=0
d) Chứng minh rằng ko có đường thẳng (d) nào đi qua điểm A(-1/2 ;1)
cần gấp =))))) thank you