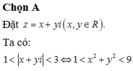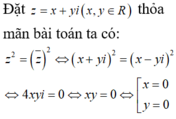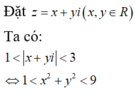Trong mặt phẳng tọa độ Oxy , biểu diễn các điểm A(0;3) , B(-4;0) , C(-2;3) , D(1/2;-3)
a) Tính diện tích tam giác ABC
b) Tìm m để đồ thị hàm số y=(2m-1)x đi qua điểm D
c) Vẽ đồ thị hàm số ứng với giá trị tìm được m ở phần b

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy , điểm biểu diễn số phức z=-4+5i có tọa độ là
A.(-4;5)
B.(-4;-5)
C.(4;-5)
D.(5;-4)
Chọn A
Trong mặt phẳng tọa độ Oxy,
điểm biểu diễn số phức z=-4+5i có tọa độ là (-4;5).
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z có phần thực bằng ‒2. A. Đường thẳng
x
+
2
0
B. Đường thẳng
y
+
2
0
C. Đường thẳng
x
-
2
0
D. Đường thẳng
y
-
2
0
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z có phần thực bằng ‒2.
A. Đường thẳng x + 2 = 0
B. Đường thẳng y + 2 = 0
C. Đường thẳng x - 2 = 0
D. Đường thẳng y - 2 = 0
Đáp án A.
Tập hợp các điểm biểu diễn số phức z có phần thực bằng ‒2 là đường thẳng x + 2 = 0 .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z có phần thực bằng ‒2.
A. Đường thẳng x + 2 = 0
B. Đường thẳng y + 2 = 0
C. Đường thẳng x - 2 = 0
D. Đường thẳng y - 2 = 0
Đáp án A.
Tập hợp các điểm biểu diễn số phức z có phần thực bằng ‒2 là đường thẳng x + 2 = 0 .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
z
2
z
2
A. Trục Ox và trục Oy B. Trục Ox C. Trục Oy D. Không có điểm M
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z 2 = z 2
A. Trục Ox và trục Oy
B. Trục Ox
C. Trục Oy
D. Không có điểm M
Trong mặt phẳng tọa độ phức Oxy, cho A,B,C là các điểm tương ứng biểu diễn các số phức
z
1
i
,
z
2
−
1
+
2
i
;
z
3
2
. Tọa độ trọng tâm tam giác ABC là A.
1
3
;
0...
Đọc tiếp
Trong mặt phẳng tọa độ phức Oxy, cho A,B,C là các điểm tương ứng biểu diễn các số phức z 1 = i , z 2 = − 1 + 2 i ; z 3 = 2 . Tọa độ trọng tâm tam giác ABC là
A. 1 3 ; 0 .
B. - 1 3 ; 1 .
C. 1 2 ; 3 2 .
D. 1 3 ; 1 .
Đáp án D
Tọa độ các điểm A,B,C tương ứng là A 0 ; 1 , B − 1 ; 2 , C 2 ; 0 .
Trong tâm G 0 − 1 + 2 3 ; 1 + 2 + 0 3 = 1 3 ; 1 .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
1
z
3
A. Phần hình phẳng nằm hoàn toàn phía ngoài hình tròn (O,1) và phía trong hình tròn (O,3) B. Hình tròn (O,3) (bỏ gốc tọa độ O) C. Hình tròn (O,1) (bỏ gốc tọa độ O) D. Đường tròn (O,1)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn 1 < z < 3
A. Phần hình phẳng nằm hoàn toàn phía ngoài hình tròn (O,1) và phía trong hình tròn (O,3)
B. Hình tròn (O,3) (bỏ gốc tọa độ O)
C. Hình tròn (O,1) (bỏ gốc tọa độ O)
D. Đường tròn (O,1)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
z
2
(
z
¯
)
2
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z 2 = ( z ¯ ) 2
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn
z
-
i
1
+
i
z
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2;-1) bán kính
R
2
B. Tập hợp các điểm biểu diễn các số phức...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn z - i = 1 + i z
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2;-1) bán kính R = 2
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;1) bán kính R = 3
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;-1) bán kính R = 3
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;-1) bán kính R = 2
Đáp án D
Đặt z = x + yi ta có
x + y i = 1 + i x + y i ⇔ x + y - 1 i = x - y x + y i
x 2 + y - 1 2 = x - y 2 + x + y 2 ⇔ x 2 + y 2 - 2 y - 1 = 0 ⇔ x 2 + y + 1 2 = 2
Vậy tập hợp các điểm biểu diễn các số phức z là đường tròn tâm bán kính R = 2
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
1
z
3
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn 1 < z < 3

![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho điểm B(-1;0) và vecto \(\overrightarrow v = \left( {0; - 7} \right)\)
a) Biểu diễn vecto \(\overrightarrow v \) qua hai vecto \(\overrightarrow i ,\overrightarrow j \)
b) Biểu diễn vecto \(\overrightarrow {OB} \) qua hai vecto\(\overrightarrow i ,\overrightarrow j \)
a) Vì \(\overrightarrow v = \left( {0; - 7} \right)\)nên \(\overrightarrow v = 0\overrightarrow i + \left( { - 7} \right)\overrightarrow j = - 7\overrightarrow j \)
b) Vì B có tọa độ là (-1; 0) nên \(\overrightarrow {OB} = \left( { - 1;{\rm{ }}0} \right)\). Do đó: \(\overrightarrow {OB} = \left( { - 1} \right)\overrightarrow i + 0\overrightarrow j = - \overrightarrow i \)
Đúng 0
Bình luận (0)