trong mặt phẳng Oxy, cho đường thẳng d: x-2y+4=0. tìm ảnh của d qua phép vị tự tâm I(1;-2) với tỉ số k= -2.

Những câu hỏi liên quan
Trong mặt phẳng Oxy cho (-7;2)và đường thẳng d:x-2y+10=0 Tìm phương trình đường thẳng d' là ảnh của d qua phép vị tự tâm I tỉ số vị tự bằng 3.
Lấy A(2;6) thuộc d
Theo đề, ta có; \(\overrightarrow{IA'}=3\cdot\overrightarrow{IA}\)
=>\(\left\{{}\begin{matrix}x+7=3\left(2+7\right)\\y-2=3\left(6-2\right)\end{matrix}\right.\Leftrightarrow A'\left(20;14\right)\)
Thay x=20 và y=14 vào (d'): x-2y+c=0, ta đc:
c+20-28=0
=>c=8
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: x + 2y – 3 = 0. Tìm ảnh của d qua phép vị tự tâm O tỉ số 2.
Trong mặt phẳng Oxy cho đường thẳng d: 3x - 2y +3 =0. Ảnh của d qua phép vị tự tâm O, tỉ số k =2 là
Gọi \(M\left(x;y\right)\) là điểm bất kì thuộc d \(\Rightarrow3x-2y+3=0\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép vị tự nói trên \(\Rightarrow M'\in d'\) với d' là ảnh của d
Ta có:
\(\left\{{}\begin{matrix}x'=2x\\y'=2y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}x'\\y=\dfrac{1}{2}y'\end{matrix}\right.\)
Thế vào (1):
\(\dfrac{3}{2}x'-y'+3=0\Leftrightarrow3x'-2y'+6=0\)
Vậy pt ảnh của d có dạng: \(3x-2y+6=0\)
Đúng 1
Bình luận (1)
d: 3x-2y+3=0
Chọn a( 1;3) thuộc d
V(O;k=2) (a)=a'
-> oa'=k.oa
x' = k .x -> x'= 2x1=2
y'= k.ý-> y'= 2x3= 6 a'(2;6)
a thuộc d' mà d' có dạng 3x'-2y'+c=0
thay a'(2;6) vào d' ta đc:
3x2-2x6+c=0
-> c= 6
vậy d' : 3x-2y+6=0
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình 2x + y − 4 = 0.
a) Hãy viết phương trình của đường thẳng d 1 là ảnh của d qua phép vị tự tâm O tỉ số k = 3
b) Hãy viết phương trình của đường thẳng d 2 là ảnh của d qua phép vị tự tâm I(1;2) tỉ số k = -2
a) Lấy hai điểm A(0;4) và B(2;0) thuộc d. Gọi A′, B′ theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có
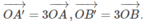
Vì O A → = ( 0 ; 4 ) nên O A ' → = ( 0 ; 12 ) . Do đó A′ = (0;12).
Tương tự B′ = (6;0); d1 chính là đường thẳng A'B' nên nó có phương trình:
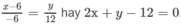
b) Có thể giải tương tự như câu a) .
Sau đây ta sẽ giải bằng cách khác.
Vì d 2 / / d nên phương trình của d 2 có dạng 2x + y + C = 0.
Gọi A′ = (x′;y′) là ảnh của A qua phép vị tự đó thì ta có:
I A ' → = − 2 I A → hay x′ + 1 = −2, y′ − 2 = −4
Suy ra x′ = −3, y′ = −2
Do A' thuộc d 2 nên 2.(−3) – 2 + C = 0.
Từ đó suy ra C = 8
Phương trình của d 2 là 2x + y + 8 = 0
Đúng 0
Bình luận (0)
4. Trong mặt phẳng Oxy, cho đường thẳng d: x − 3y + 1 = 0 và điểm I(−3; 1).
(a) Tìm ảnh của điểm M(1; −2) qua phép đối xứng tâm I.
(b) Tìm ảnh của đường thẳng ∆: 2x + y − 1 = 0 qua phép đối xứng tâm I.
(c) Tìm ảnh của đường tròn (C): (x − 2)2 + (y + 3)2 = 9 qua phép đối xứng
Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d có phương trình x+2y+30. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được từ việc thực hiện liên tiếp phép quay tâm O góc quay -
90
∘
và phép vị tự tâm O tỉ số 5. A. d : 2x-y-150 B. d : 2x-y+150 C. d : 2x-y+
3
5
0 B. d : x-y+300
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d có phương trình x+2y+3=0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được từ việc thực hiện liên tiếp phép quay tâm O góc quay - 90 ∘ và phép vị tự tâm O tỉ số 5.
A. d' : 2x-y-15=0
B. d' : 2x-y+15=0
C. d' : 2x-y+ 3 5 =0
B. d' : x-y+30=0
Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d có phương trình
x
+
2
y
+
3
0
. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được từ việc thực hiện liên tiếp phép quay tâm O góc quay
−
90
°
và phép vị tự tâm O tỉ số 5. A.
d
:
2
x
−
y
−
15
0...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d có phương trình x + 2 y + 3 = 0 . Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được từ việc thực hiện liên tiếp phép quay tâm O góc quay − 90 ° và phép vị tự tâm O tỉ số 5.
A. d ' : 2 x − y − 15 = 0
B. d ' : 2 x − y + 15 = 0
C. d ' : 2 x − y + 3 5 = 0
D. d ' : x + 2 y − 30 = 0
Đáp án B
d cắt Ox,Oy lần lượt tại A − 3 ; 0 ; B 0 ; − 3 2 Qua phép quay tâm O góc quay − 90 ° điểm A và B lần lượt biến thành các điểm A ' 0 ; 3 ; B − 3 2 ; 0 ⇒ A ' B ' : 2 x − y + 3 = 0
Phép vị tự biến đường thẳng thành đường thẳng song song với nó nên d ' : 2 x − y + m = 0
Qua V O ; k A ' = A 1 ⇒ O A 1 → = 5 O A ' → ⇒ A 1 0 ; 15 ⇒ d ' : 2 x − y + 15 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x+y-20. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
I
(
-
1
;
-
1
)
tỉ số k
1
2
và phép quay tâm O góc
-
45
∘
A. y0 B. y-x C. yx D. x0
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x+y-2=0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I ( - 1 ; - 1 ) tỉ số k= 1 2 và phép quay tâm O góc - 45 ∘
A. y=0
B. y=-x
C. y=x
D. x=0
Trong mặt phẳng Oxy cho đường thẳng d có phương trình
x
+
y
−
2
0
. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
I
−
1
;
−
1
tỉ số
k
1
2
và phép quay tâm O góc
−...
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y − 2 = 0 . Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I − 1 ; − 1 tỉ số k = 1 2 và phép quay tâm O góc − 45 °
A. y=0
B. y= -x
C. y=x
D.x=0
Đáp án D
Ta có V I , 1 2 biến M 0 ; 2 ∈ d thành M ' x ' ; y ' thì I M ' → = 1 2 I M → ⇔ x ' = − 1 2 y ' = 1 2
V I , 1 2 biến đường thẳng d thành đường thẳng đi qua M ' − 1 2 ; 1 2 , có cùng vtpt 1 ; 1 và có phương trình là x + 1 2 + y − 1 2 = 0 ⇔ x + y = 0
Phép quay tâm O góc quay − 45 ° biến điểm N x ; y thuộc đường thẳng x + y = 0 thành điểm
N ' x ' ; y ' ∈ d ' ⇒ x = x ' cos 45 ° − y ' sin 45 ° y = x ' sin 45 ° + y ' cos 45 ° ⇒ x = 2 2 x ' − y ' y = 2 2 x ' + y ' *
Thay (*) vào x + y = 0 ta được x ' = 0 ⇒ d ' : x = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng d có phương trình
x
+
y
−
2
0
. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
I
−
1
;
−
1
tỉ số
k
1
2
và phép quay tâm O góc
−...
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y − 2 = 0 . Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I − 1 ; − 1 tỉ số k = 1 2 và phép quay tâm O góc − 45 °
A.y=0
B. y=-x
C. y=x
D. x=0
Đáp án D
Ta có V I , 1 2 biến M 0 ; 2 ∈ d thành M ' x ' ; y ' thì I M ' → = 1 2 I M → ⇔ x ' = − 1 2 y ' = 1 2
V I , 1 2 biến đường thẳng d thành đường thẳng đi qua M ' − 1 2 ; 1 2 , có cùng vtpt 1 ; 1 và có phương trình là x + 1 2 + y − 1 2 = 0 ⇔ x + y = 0
Phép quay tâm O góc quay − 45 ° biến điểm N x ; y thuộc đường thẳng x + y = 0 thành điểm
N ' x ' ; y ' ∈ d ' ⇒ x = x ' cos 45 ° − y ' sin 45 ° y = x ' sin 45 ° + y ' cos 45 ° ⇒ x = 2 2 x ' − y ' y = 2 2 x ' + y ' *
Thay * vào x + y = 0 ta được x ' = 0 ⇒ d ' : x = 0
Đúng 0
Bình luận (0)














