Mệnh đề nào sau đây đúng?
(1) Đường tròn (C1) : x2+ y2 – 2x +4y - 4= 0 có tâm I( 1; -2) bán kính R= 3.
(2) Đường tròn (C2) x2+ y2 – 5x +3y – 0,5= 0 có tâm bán I 5 2 ; - 3 2 kính R= 3.
A. Chỉ (1).
B. Chỉ (2).
C.cả hai
D. Không có.
Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:
2x2 + y2 – 8x + 2y – 1 = 0;
x2 + y2 + 2x – 4y – 4 = 0;
x2 + y2 – 2x – 6y + 20 = 0;
x2 + y2 + 6x + 2y + 10 = 0.
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.
a) x2 + y2 + xy + 4x – 2 = 0;
b) x2 + y2 – 2x – 4y + 5 = 0;
c) x2 + y2 + 6x – 8y + 1 = 0.
a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).
Trong hệ tọa độ Oxy, cho hai đường tròn có phương trình (C1) : x2+ y2- 4y -5 = 0 và (C2) : x2+ y2- 6x + 8y +16= 0 . Phương trình nào sau đây là tiếp tuyến chung của 2 đường tròn.
![]()
![]()
![]()
D. Đáp án khác.
Đáp án D
- Ta có :
(C1) tâm I1(0;2) và R1= 3; (C2) tâm I2( 3;-4) và R2= 3
- Nhận xét : ![]() không cắt C2
không cắt C2
- Gọi d: ax+ by+ c= 0 là tiếp tuyến chung , thế thì : d(I1; d) = R1 và d (I2; d) = R2
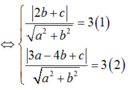
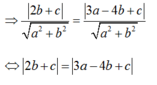
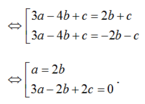
- Trường hợp: a= 2b thay vào (1):
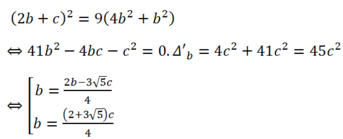
- Do đó ta có hai đường thẳng cần tìm :
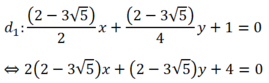
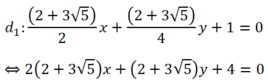
- Trường hợp : 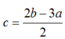 thay vào :
thay vào : 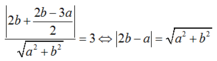
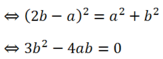

-Có 2 đường thẳng : d3: 2x- 1 = 0 và d4: 6x + 8y -1= 0.
Có tất cả 4 tiếp tuyến chung.
Bài tập :
B1 Viết phương trình đường tròn (C1) có bán kính R1 = 1 , tiếp xúc với trục Ox và có tâm nằm trên đường thẳng denta : 3x - y +7 = 0
B2 Cho đường tròn (C) : x2 + y2 - 2x - 4y - 4 = 0 và đường thẳng (d) : 3x + 4y +4 = 0 . Chứng minh rằng (d) tiếp xúc với (C)
Trong không gian Oxyz, cho mặt cầu
S = x 2 + y 2 + z 2 + 4 y - 2 z - 4 = 0
và mặt phẳng (a): x + y + 2z - 8 = 0. Mệnh đề nào sau đây đúng?
A. (a) cắt (S) theo một đường tròn
B. (a) tiếp xúc với (S).
C. (a) qua tâm I của (S)
D. (a) và (S) không có điểm chung.
(S) có tâm I ( 0;-2;1 ) và bán kính R = 3
Ta có d ( I; (a) ) = - 2 + 2 - 6 = 4 6 3 > R = 3
Vậy (a) không cắt mặt cầu (S).
Đáp án D
Số tiếp tuyến chung của hai đường tròn ( C 1 ) : x 2 + y 2 - 2 x + 4 y + 1 = 0 v à ( C 2 ) : x 2 + y 2 + 6 x - 8 y + 20 = 0
A. 1
B. 2
C. 3
D. 4
Cho đường tròn (C) : x2+ y2+ 8x+ 6y+ 9= 0. Mệnh đề nào sau đây sai?
A. (C) không đi qua điểm O.
B. tâm I( -4; -3).
C.bán kính R= 4.
D. (C) đi qua điểm M(-1; 0) .
+Ta có a= -4; b= -3 ; c= 9 và a2+ b2- c= 16+ 9 - 9 = 16> 0
Suy ra (C) là đường tròn tâm I( -4; -3) và R= 4
Vậy B; C đúng.
+Thay O vào (C) ta có: 02+ 02+ 8.0+ 6.0 + 9= 0 vô lí . Vậy A đúng.
+Thay M( -1; 0) vào (C) ta có: (-1) 2+ 02+ 8.(-1) + 6.0 + 9= 0 ( vô lý). Vậy D sai.
Chọn D.
Cho đường tròn (C) : x2+ y2- 4x + 3= 0 . Hỏi mệnh đề nào sau đây sai?
A. tâm I( 2; 0)
B. bán kính R= 1
C. (C) cắt trục 0x tại 2 điểm.
D. (C) cắt trục Oy tại 2 điểm.
Cho x= 0 ta được: y2+ 3= 0 phương trình vô nghiệm.
Vậy (C) không có điểm chung nào với trục tung.
Chọn D.
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): x 2 + y 2 - 2 x - 4 y + 4 = 0 và đường tròn (C'): x 2 + y 2 + 6 X + 4 y + 4 = 0 Tìm tâm vị tự của hai đường tròn?
A. I(0;1) và J(3;4)
B. I(-1;-2) và J(3;2)
C. I(1;2) và J(-3;-2)
D. I(1;0) và J(4;3)