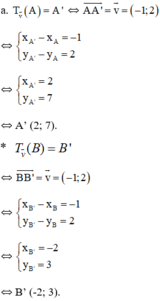
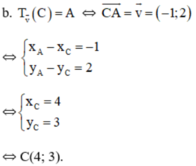
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)

=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d

=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.

Nên đường thẳng d’ có dạng : x- 2y + m= 0

Lại có B(-1; 1) d nên B’(-2;3) d’

Thay tọa độ điểm B’ vào phương trình d’ ta được:

-2 -2.3 +m =0 ⇔ m= 8

Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0

(C) có \(\left\{{}\begin{matrix}I\left(2;3\right)\\R=3\end{matrix}\right.\)

\(T_{\overrightarrow{v}}\left(I\right)=I'\left(x',y'\right)\)\(\Rightarrow\left\{{}\begin{matrix}x'=x+a=2+\left(-1\right)=1\\y'=y+a=3+2=5\end{matrix}\right.\Rightarrow I'\left(1,5\right)\)

\(T_{\overrightarrow{v}}\left(C\right)=\left(C'\right)\) có \(\left\{{}\begin{matrix}I'\left(1,5\right)\\R=3\end{matrix}\right.\)

\(\Rightarrow\) \(\left(C'\right):\left(x-1\right)^2+\left(y-5\right)^2=3\)

\(T_{\overrightarrow{v}}\left(N\right)=M\Rightarrow\overrightarrow{NM}=\overrightarrow{v}\)

\(\Rightarrow\left\{{}\begin{matrix}x_N+3=-4\\y_N-1=2\end{matrix}\right.\) \(\Rightarrow N\left(-7;3\right)\)

Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=3\)

Ảnh của đường tròn (C) là đường tròn (C') có tâm \(I'\left(x';y'\right)\) là ảnh của I qua phép tịnh tiến \(\overrightarrow{v}\) và bán kính \(R'=R=3\)

\(\left\{{}\begin{matrix}x'=-3+1=-2\\y'=1-2=-1\end{matrix}\right.\)

Phương trình (C'):

\(\left(x+2\right)^2+\left(y+1\right)^2=9\)

\(T_{\overrightarrow{v}}\left(N\right)=M\left(x',y'\right)\)

\(\Rightarrow\left\{{}\begin{matrix}x'=x+a=-3+4=1\\y'=y+b=10+1=11\end{matrix}\right.\)

\(\Rightarrow M\left(1;11\right)\)