Cho z1; z2 là hai nghiệm phức của phương trình z2 - 2z + 4 = 0. Tìm phần thực, phần ảo của số phức: 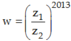 lần luợt là bao nhiêu, biết z1 có phần ảo dương.
lần luợt là bao nhiêu, biết z1 có phần ảo dương.
A. 0; 1
B. 1; 2
C. 1; 0
D. tất cả sai
Cho z 1 , z 2 ∈ C. Khẳng định nào sau đây là sai?
A. z 1 . z 2 + z 1 . z 2 ∈ R.
B. z 1 . z 2 + z 1 . z 2 ∈ R
C. z 1 . z 2 . z 1 . z 2 ∈ R
D. z 1 . z 2 - z 1 . z 2 ∈ R
Đáp án: D
z ∈ R ⇔ z = z , ( z 1 + z 2 )= z 1 + z 2 , ( z 1 . z 2 )= z 1 . z 2
Cho số phức z 1 , z 2 thỏa mãn z 1 + z 2 = 3 , z 1 = 1 , z 2 = 2 . Tính z 1 . z 2 ¯ + z 1 ¯ . z 2
A. 2
B. 8
C. 9
D. 4
Cho 2 số phưc z1 , z2 thỏa |z1 - 20| ^2 + Cho |z1-10i|^2 =√(|z2 -20|^2 + | z2 -10i|^2). Và |z1 -20| +|z1 -10i| =10√5 . tìm giá trị lớn nhất của |z1 -z2|
Cho z1, z2 ∈ C. Khẳng định nào sau đây là sai?
A. z1. z 2 + z 1 .z2 ∈ R.
B. z1.z2 + z 1 . z 2 ∈ R
C. z1. z 2 . z 2 .z2 ∈ R
D. z1.z2 - z 2 .z−2 ∈ R
Đáp án: D.
z ∈ R ⇔ z = z , (z1 + z 2 ) = z 1 + z 2 , (z1. z 2 ) = z−1. z 2 .
Cho hai số phức z 1 , z 2 thỏa mãn z 1 - 20 + z 1 - 10 i = z 2 - 20 2 + z 2 - 10 i 2 và z 1 - 20 + z 1 - 10 i = 10 5 . Giá trị lớn nhất của z 1 - z 2 là
A. 20
B. 40
C. 30
D. 10 5
Cho hai số phức z 1 , z 2 thỏa mãn z 1 = z 2 = 1 ; z 1 + z 2 = 3 . Tính z 1 - z 2 .
A. 4
B. 3
C. 2
D. 1
Đặt z 1 = x 1 + i y 1 , z 2 = x 2 + i y 2 .
Từ giả thiết ta suy ra
x 1 2 + y 1 2 = x 2 2 + y 2 2 = 1 x 1 + x 2 2 + y 1 + y 2 2 = 3 ⇒ 2 x 1 y 1 + x 2 y 2 = 1
Suy ra:
z 1 - z 2 2 = x 1 - x 2 2 + y 1 - y 2 2 = x 1 - x 2 2 + y 1 - y 2 2 - 4 x 1 y 1 + x 2 y 2 = 3 - 2 = 1
Vậy z 1 - z 2 = 1
Đáp án D
Cho hai số phức z 1 , z 2 thỏa mãn | z 1 - 20 | + | z 1 - 10 i | = √ ( | z 2 - 20 | 2 + | z 2 - 10 i | 2 ) và | z 1 - 20 | + | z 1 - 10 i | = 10 5 . Giá trị lớn nhất của | z 1 - z 2 | là
A. 20
B. 40
C. 30
D. 10 5
Cho hai số phức z 1 , z 2 thỏa mãn | z 1 | = | z 2 | = | z 1 + z 2 | = 1 . Khi đó | z 1 - z 2 | bằng
A. 0
B. 1
C. 2
D. 3
Cho các số phức z 1 , z 2 thỏa mãn z 1 + z 2 = 3 , z 1 = z 2 = 1 . Tính z 1 z 2 ¯ + z 1 ¯ z 2
![]()
![]()
![]()
![]()
Cho các số phức z 1 , z 2 thỏa mãn z 1 = z 2 = 3 và z 1 - z 2 = 2 . Môđun z 1 + z 2 bằng
A. 2
B. 3
C. 2
D. 2 2
Cách 1:
Gọi các số phức
z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i ( a 1 , b 1 , a 2 , b 2 ∈ ℝ )
z 1 - z 2 = a 1 - a 2 + b 1 - b 2 i z 1 + z 2 = a 1 + a 2 + b 1 + b 2 i
Ta có: z 1 = a 1 2 + b 1 2 = 3
⇒ a 1 2 + b 1 2 = 3
z 2 = a 2 2 + b 2 2 = 3 ⇒ a 2 2 + b 2 2 = 3
z 1 - z 2 = 2
⇔ a 1 - a 2 2 + b 1 - b 2 2 = 2 ⇔ a 1 - a 2 2 + b 1 - b 2 2 = 4 ⇔ a 1 2 + b 1 2 + a 2 2 + b 2 2 - 2 a 1 a 2 - 2 b 1 b 2 = 4 ⇔ 2 a 1 a 2 + 2 b 1 b 2 = 2
Do đó:
z 1 + z 2 = a 1 + a 2 2 + b 1 + b 2 2 = a 1 2 + b 1 2 + a 2 2 + b 2 2 + 2 a 1 a 2 + 2 b 1 b 2 = 8 = 2 2
Cách 2:
z 1 - z 2 2 = z 1 - z 2 z 1 ¯ - z 2 ¯ = z 1 2 + z 2 2 - z 1 z 2 ¯ + z 2 z 1 ¯ = 4 z 1 + z 2 2 = z 1 + z 2 z 1 ¯ + z 2 ¯ = z 1 2 + z 2 2 + z 1 z 2 ¯ + z 2 z 1 ¯ = 8 ⇒ z 1 + z 2 = 2 2
Cách 3:
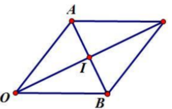
Gọi A, B lần lượt là điểm biểu diễn 2 số phức z 1 , z 2 . Khi đó tam giác OAB có O A = O B = 3 , A B = 2 . Gọi I là trung điểm của AB.
O I = O A 2 - A I 2 = 2 z 1 + z 2 = 2 O I ⇀ = 2 2
Chọn đáp án D.