Question

Cho các số phức z 1 , z 2  thỏa mãn z 1 = z 2 = 3  và z 1 - z 2 = 2 . Môđun z 1 + z 2  bằng

A. 2

B. 3

C.  2

D.  2 2

Answer 1

Cách 1:

Gọi các số phức

z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i   ( a 1 , b 1 , a 2 , b 2 ∈ ℝ )

z 1 - z 2 = a 1 - a 2 + b 1 - b 2 i z 1 + z 2 = a 1 + a 2 + b 1 + b 2 i

Ta có: z 1 = a 1 2 + b 1 2 = 3

⇒ a 1 2 + b 1 2 = 3

z 2 = a 2 2 + b 2 2 = 3 ⇒ a 2 2 + b 2 2 = 3

z 1 - z 2 = 2

⇔ a 1 - a 2 2 + b 1 - b 2 2 = 2 ⇔ a 1 - a 2 2 + b 1 - b 2 2 = 4 ⇔ a 1 2 + b 1 2 + a 2 2 + b 2 2 - 2 a 1 a 2 - 2 b 1 b 2 = 4 ⇔ 2 a 1 a 2 + 2 b 1 b 2 = 2

Do đó:

z 1 + z 2 = a 1 + a 2 2 + b 1 + b 2 2 = a 1 2 + b 1 2 + a 2 2 + b 2 2 + 2 a 1 a 2 + 2 b 1 b 2 = 8 = 2 2

Cách 2:

z 1 - z 2 2 = z 1 - z 2 z 1 ¯ - z 2 ¯ = z 1 2 + z 2 2 - z 1 z 2 ¯ + z 2 z 1 ¯ = 4 z 1 + z 2 2 = z 1 + z 2 z 1 ¯ + z 2 ¯ = z 1 2 + z 2 2 + z 1 z 2 ¯ + z 2 z 1 ¯ = 8 ⇒ z 1 + z 2 = 2 2

Cách 3:

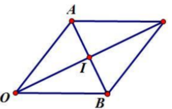
Gọi A, B lần lượt là điểm biểu diễn 2 số phức z 1 , z 2 . Khi đó tam giác OAB có O A = O B = 3 ,   A B = 2 . Gọi I là trung điểm của AB.

O I = O A 2 - A I 2 = 2 z 1 + z 2 = 2 O I ⇀ = 2 2

Chọn đáp án D.