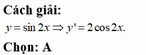Trong bốn hàm sô: y=sin2x; y=cos4x; y=tan2x; y=cot3x có mấy hàm số tuần hoàn với chu kì pi/2

Những câu hỏi liên quan
Cho bốn hàm số:
1
y
sin
2
x
;
2
y
cos
4
x
;
3
y
tan
2
x
;
4
y
cot
3
x
Có mấy hàm số tuần hoàn với chu kì
π
2
?
A. 0 B. 2 C. 3 D. 1
Đọc tiếp
Cho bốn hàm số:
1
y
=
sin
2
x
;
2
y
=
cos
4
x
;
3
y
=
tan
2
x
;
4
y
=
cot
3
x
Có mấy hàm số tuần hoàn với chu kì
π
2
?
A. 0
B. 2
C. 3
D. 1
trong các hàm số sau đây , hàm số nào không tuần hoàn
a. y= x.sin x
b. y= cos 2x
c. y=sin(x-x/2)
d. y=1/sin2x
Hàm \(y=x.sinx\) không phải hàm tuần hoàn
Đúng 1
Bình luận (2)
Trong các cặp hàm số dưới đây, hàm số nào là nguyên hàm của hàm số còn lại? sin 2 x v à sin sin 2 x
Đạo hàm của hàm số y cos6x + sin4x. cos2x + sin2x. cos4x + sin4x – sin2x bằng biểu thức nào sau đây? A.
-
6
cos
5
x
sin
x
B.
6
cos
5
x
sin
x
C.
6
sin
5
x
cos
x
D.
6
cos
5...
Đọc tiếp
Đạo hàm của hàm số y = cos6x + sin4x. cos2x + sin2x. cos4x + sin4x – sin2x bằng biểu thức nào sau đây?
A. - 6 cos 5 x sin x
B. 6 cos 5 x sin x
C. 6 sin 5 x cos x
D. 6 cos 5 x
Chọn A
y = cos6 x+ sin2xcos2x(sin2x + cos2x) + sin4x - sin2x
= cos6x + sin2x(1 - sin2x) + sin4x - sin2x = cos6x
Do đó : y' = -6cos5xsinx.
Đúng 0
Bình luận (0)
Tìm cực trị của các hàm số sau:
a) y = sin2x
b) y = cosx − sinx
c) y = sin 2 x
a) y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔ 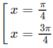
Bảng biến thiên:
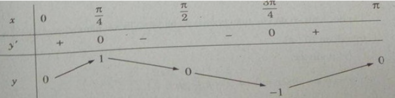
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và y C D = y(π/4) = 1; y C T = y(3π/4) = −1
Vậy trên R ta có:
y C Đ = y(π/4 + kπ) = 1;
y C T = y(3π/4 + kπ) = −1, k∈Z
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
Lập bảng biến thiên trên đoạn [−π;π]
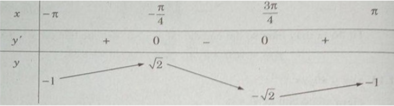
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
y C Đ = y(−π4 + k2π) = 2 ;
y C T = y(3π4 + k2π) = − 2 (k∈Z).
c) Ta có:
![]()
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
Ta xét hàm số y trên đoạn [0;π]:
![]()
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
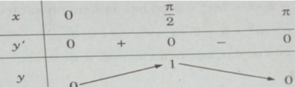
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
y C T = y(2mπ) = 0; yCT = y(2mπ) = 0;
y C Đ = y((2m+1)π/2) = 1 (m∈Z)
Đúng 0
Bình luận (0)
Đạo hàm của hàm số y sin2x là: A.
y
2
cos
2
x
B.
y
cos
2
x
C.
y
2
cos
x
D.
y
-
2
cos
2
x
.
Đọc tiếp
Đạo hàm của hàm số y = sin2x là:
A. y ' = 2 cos 2 x
B. y ' = cos 2 x
C. y ' = 2 cos x
D. y ' = - 2 cos 2 x .
Tính đạo hàm hàm số
y
sin
2
x
−
cos
x
A.
y
2
cos
2
x
+
sin
x
B.
y
2
cos
x
−
sin
x
C.
y
2
sin
x
+
cos
2...
Đọc tiếp
Tính đạo hàm hàm số y = sin 2 x − cos x
A. y ' = 2 cos 2 x + sin x
B. y ' = 2 cos x − sin x
C. y ' = 2 sin x + cos 2 x
D. y ' = 2 cos x + sin x
Tính đạo hàm hàm số
y
sin
2
x
−
cos
x
A.
y
2
cos
2
x
+
sin
x
B.
y
2
cos
x
−
sin
x
C.
y
2
sin
x
+
cos
2...
Đọc tiếp
Tính đạo hàm hàm số y = sin 2 x − cos x
A. y ' = 2 cos 2 x + sin x
B. y ' = 2 cos x − sin x
C. y ' = 2 sin x + cos 2 x
D. y ' = 2 cos x + sin x
Đạo hàm của hàm số y=sin2x là:
A. y’=2cos2x
B. y’=cos2x
C. y’=2cosx
D. y’=-2cos2x
Cho hàm số y = sin2x - 2x. Hàm số này
A. Luôn đồng biến trên R
B. Chỉ đồng biến trên khoảng (0; +∞)
C. Chỉ nghịch biến trên (-∞; -1)
D. Luôn nghịch biến trên R
Tập xác định D = R
Ta có : y' = 2.cos2x - 2 = 2(cos2x - 1) ≤ 0; ∀ x
(vì -1 ≤ cos2x ≤ 1)
Vậy hàm số luôn nghịch biến trên R
Chọn đáp án D.
Đúng 0
Bình luận (0)