a, Vẽ parabol (P); y= 1/2x2 và đường thẳng (d): y= 3/2x-1 trên cùng mặt phẳng tọa độ
b, Xác định tọa độ giao điểm của (P) và (d) bằng phép toán.
Cho parabol ( P ) : y = x2 và đường thẳng ( d ) : y = ( 2 -m )x + m2 + 1 .
a/ Vẽ parabol ( P ) .
b/ Chứng minh rằng parabol ( P ) và đường thẳng ( d ) luôn cắt nhau tại hai điểm phân biệt A và B .
b: Phương trình hoành độ giao điểm là:
\(x^2+\left(m-2\right)x-m^2-1=0\)
\(ac=-m^2-1< 0\)
Do đó: (P) luôn cắt (d) tại hai điểm phân biệt
Cho parabol (P): y=x2
1. Vẽ parabol (P)
2. Với giá trị nào của m thì điểm A(2m-1;9) nằm trên parabol (P)
Cho parabol y=\(\frac{2}{3}x^2+1\) và y=5x-3
a) vẽ 2 parabol
b)Tìm tọa độ giao điểm 2 parabol
Trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x2 và đường thẳng (d): y=2(m-1)x+5-2m (m là tham số)
a) Vẽ đồ thị parabol (P).
b) Biết đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt. Gọi hoành độ giao điểm của đường thẳng (d) và parabol (P) là x1, x2. Tìm m để x+x=6
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4
a) Giải hệ phương trình
2x+2y=7
2x-2y=3
b) Cho hàm số y = x2 có đồ thị là parabol (p). Vẽ parabol (p) trên mặt phẳng tọa độ Oxy.
a) Giải hệ phương trình
2x+2y=7
2x-2y=3
b) Cho hàm số y = x2 có đồ thị là parabol (p). Vẽ parabol (p) trên mặt phẳng tọa độ Oxy.
a: =>4x=10 và x-y=3/2
=>x=5/2 và y=1
b: 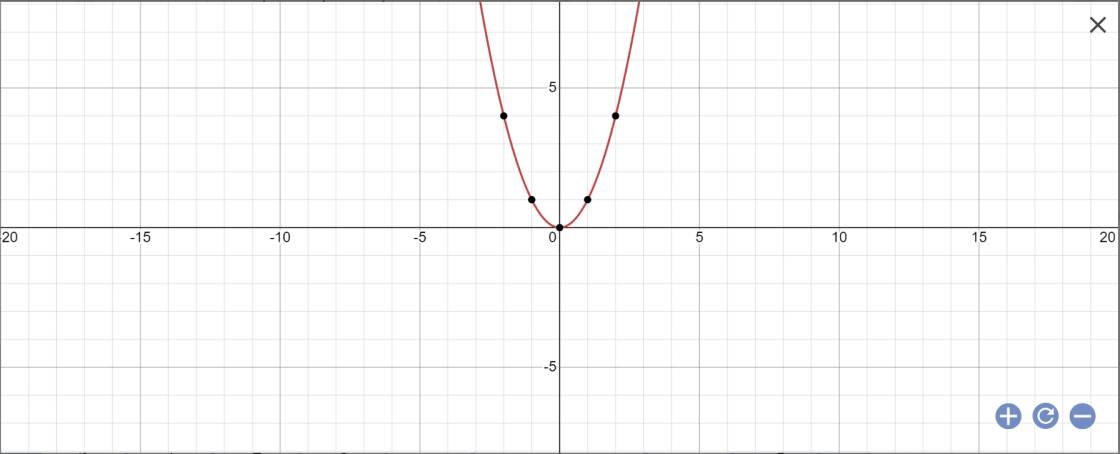
Vẽ parabol
a. ( P ) : y = 3x^2 - 2x - 1
Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = 1/2x2
a) Vẽ đồ thị parabol (P).
a) Tìm a và b để đường thẳng (d): y = a.x + b đi qua điểm (0;-1) và tiếp xúc với (P).
b) Để (d) đi qua (0;-1) thì
Thay x=0 và y=-1 vào y=ax+b, ta được:
\(a\cdot0+b=-1\)
\(\Leftrightarrow b=-1\)
Vậy: (d): y=ax-1
Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=ax-1\)
\(\Leftrightarrow\dfrac{1}{2}x^2-ax+1=0\)
\(\Delta=a^2-4\cdot\dfrac{1}{2}\cdot1=a^2-2\)
Để (d) và (P) tiếp xúc với nhau thì \(\Delta=0\)
\(\Leftrightarrow a^2=2\)
hay \(a\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
Vậy: Để (d) tiếp xúc với (P) và (d) đi qua (0;-1) thì \(\left(a,b\right)=\left\{\left(\sqrt{2};-1\right);\left(-\sqrt{2};-1\right)\right\}\)
a) Vẽ parabol (P) :y =\(2x^2\)
b) Viết phương trình đường thẳng (d) cắt parabol (P) tại hai điểm A và B có hoành độ lần lượt là -1 và 2
a) Ta có bảng giá trị tương ứng x và y sau :
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 2x2 | 18 | 8 | 2 | 0 | 2 | 8 | 18 |

Quả parabol hơi xấu tí thông cảm =))
Trong mặt phẳng tọa độ Oxy, cho Parabol P : y = 2 x 2 . Vẽ đồ thị parabol (P).
a) Vẽ Parabol P : y = 2 x 2
Bảng giá trị giữa x và y:
x |
-2 |
-1 |
0 |
1 |
2 |
y |
8 |
2 |
0 |
2 |
8 |
Vẽ đúng đồ thị