Đường thẳng AB nhận \(\overrightarrow{n}=\left(1;2\right)\) làm vecto pháp tuyến

AB đi qua A (1; -1) nên nó có phương trình là

x - 1 + 2 (y + 1) = 0 hay x + 2y + 1 = 0

Gọi M là trung điểm của AB ⇒ M ∈ Δ, tọa độ của M có dạng

M (t ; 2t + 1) với t là số thực và \(\overrightarrow{AM}=\left(t-1;2t+2\right)\)

⇒ AM ⊥ Δ 

⇒ \(\overrightarrow{AM}.\overrightarrow{n}=0\)

⇒ t + 1 + 2. (2t + 2) = 0

⇒ t = -1

Vậy M (- 1; - 1)

M là trung điểm của AB => Tọa độ B

Làm tương tự như thế sẽ suy ra tọa độ C

\(cosB=\dfrac{\left|1.2+\left(-7\right).1\right|}{\sqrt{1^2+\left(-7\right)^2}.\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{10}}\)

Gọi vtpt của AC có tọa độ \(\left(a;b\right)\)

\(\Rightarrow cosC=cosB=\dfrac{1}{\sqrt{10}}=\dfrac{\left|2a+b\right|}{\sqrt{a^2+b^2}.\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{10}}\)

\(\Leftrightarrow\sqrt{2}\left|2a+b\right|=\sqrt{a^2+b^2}\)

\(\Leftrightarrow2\left(2a+b\right)^2=a^2+b^2\)

\(\Leftrightarrow7a^2+8ab+b^2=0\Leftrightarrow\left(a+b\right)\left(7a+b\right)=0\)

Chọn \(a=1\Rightarrow\left[{}\begin{matrix}b=-1\\b=-7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(1;-1\right)\\\left(a;b\right)=\left(1;-7\right)\end{matrix}\right.\)

(Trường hợp \(\left(a;b\right)=\left(1-;7\right)\) loại do khi đó AC song song AB, vô lý)

\(\Rightarrow\) Phương trình AC: \(1\left(x-4\right)-1\left(y-0\right)=0\)

Giả sử MN:  y   =   a x   +   b

Ta có N thuộc MN   0   =   a . 1   +   b   ⇔   a   =   − b

M thuộc MN   1   =   a . 0   +   b ⇔     b   =   2   ⇔   a   =   − 2   ⇒   b   =   2

Do đó MN:  y   =   − 2 x   +   2

Vì M, N lần lượt là trung điểm của các cạnh BC, CA của tam giác ABC nên MN là đường trung bình của tam giác ABC  MN // AB

Suy ra AB có dạng:  y   =   − 2 x   +   b ’   ( b ’   ≠   2 )

Vì P là trung điểm của AB nên AB đi qua P (−1; −1 )

⇔   − 1   =   − 2   ( − 1 )   +   b ’   ⇒   b ’   =   − 3   ( t / m )

Vậy AB:  y   =   − 2 x   –   3

Đáp án cần chọn là: C

A là giao của (d1) và (d2) nên tọa độ A là nghiệm:

\(\left\{{}\begin{matrix}2x+y-11=0\\x+4y-2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=-1\end{matrix}\right.\) \(\Rightarrow A\left(6;-1\right)\)

B là giao của (d1) và (d3) nên tọa độ B là nghiệm:

\(\left\{{}\begin{matrix}2x+y-11=0\\2x-2y+8=0\end{matrix}\right.\) \(\left\{{}\begin{matrix}x=2\\y=7\end{matrix}\right.\) \(\Rightarrow B\left(2;7\right)\)

C là giao của (d2) và (d3) nên tọa độ C là nghiệm:

\(\left\{{}\begin{matrix}x+4y-2=0\\3x-2y+8=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\) \(\Rightarrow C\left(-2;1\right)\)

ai biêt

Đáp án A

Trực tâm H là giao điểm của BH và AH ⇒ tọa độ H là nghiệm của hệ:

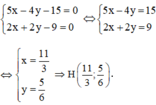
A là giao điểm của AB và AH nên tọa độ A là nghiệm của hệ phương trình:

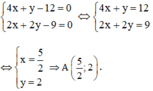
B là giao điểm BH và AB nên tọa độ điểm B là nghiệm của hệ:

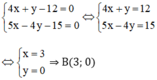
+ AC ⊥ HB, mà HB có một vtpt là (5; -4)⇒ AC nhận (4; 5) là một vtpt

AC đi qua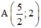 

⇒ Phương trình đường thẳng AC: 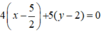 hay 4x + 5y – 20 = 0.

+ CH ⊥ AB, AB có một vtpt là (4; 1) ⇒ CH nhận (1; -4) là một vtpt

CH đi qua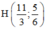 

⇒ Phương trình đường thẳng CH: 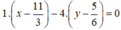 hay CH: 3x – 12y - 1 = 0.

+ BC ⊥ AH , mà AH nhận (2; 2) là một vtpt

⇒ BC nhận (1; -1) là một vtpt

BC đi qua B(3; 0)

⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y – 0) = 0 hay x – y – 3 = 0.

Giả sử I(xI;yI) là trung điểm của AC

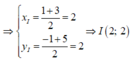
Vì tam giác ABC cân tại B nên BI ⊥ AC. Phương trình đường thẳng BI đi qua I(2;2) nhận 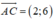 làm VTPT là:

2.(x - 2) + 6.(y - 2) = 0 ⇔ 2x - 4 + 6y - 12 = 0 ⇔ 2x + 6y - 16 = 0 ⇔ x + 3y - 8 = 0

Tọa độ giao điểm B của BI và d là nghiệm của hệ phương trình:

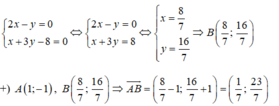
Phương trình đường thẳng AB đi qua A(1;-1) nhận 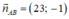 làm VTPT là:

23.(x - 1) - 1.(y + 1) = 0 ⇔ 23x - 23 - y - 1 = 0 ⇔ 23x - y - 24 = 0

⇒ a = 23; b = -1

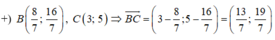
Phương trình đường thẳng BC đi qua C(3;5) nhận 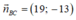 làm VTPT là:

19.(x - 3) + (-13).(y - 5) = 0 ⇔ 19x - 57 - 13y + 65 = 0 ⇔ 19x - 13y + 8 = 0

⇒ c = 19; d = -13

⇒ a.b.c.d = 23.(-1).19.(-13) = 5681

Vậy a.b.c.d = 5681.