Với mỗi trường hợp sau, hãy đoán xem đơn thức A có chia hết cho đơn thức B không; nếu chia hết, hãy tìm thương của phép chia A cho B và giải thích cách làm:
a) \(A = 6{x^3}y,B = 3{x^2}y\)
b) \(A = {x^2}y,B = x{y^2}\)
Cho đa thức A = 1 3 x 2 y 3 + y 6 + x 5 y 8 đơn thức B = 2x . Không làm tính chia, hãy xét xem đa thức A có chia hết cho đơn thức B hay không?
A. Không
B. Có
C. Chưa thể kết luận
D. Tất cả sai
Hạng tử y 6 của đa thức A không chia hết cho đơn thức B = 2x.
Do đó, đa thức A không chia hết cho đơn thức B
Chọn đáp án A
Không làm tính chia, hãy xét xem đa thức A có chia hết đơn thức B không:
A = 15xy2 + 17xy3 + 18y2
B = 6y2
Nhận thấy:
15xy2 chia hết cho 6y2
17xy3 chia hết cho 6y2
18y2 chia hết cho 6y2
Vậy A = 15xy2 + 17xy3 + 18y2 chia hết cho 6y2 hay A chia hết cho B.
Cho đa thức \(A = 9x{y^4} - 12{x^2}{y^3} + 6{x^3}{y^2}\). Với mỗi trường hợp sau đây, xét xem A có chia hết cho đơn thức B hay không? Thực hiện phép chia trong trường hợp A chia hết cho B.
a) \(B = 3{x^2}y\)
b) \(B = - 3x{y^2}\)
a) Không vì hạng tử \( 9x{y^4}\) có số mũ của biến x nhỏ hơn số mũ của biến x trong B.
b) Có. \(\begin{array}{l}A:B = \left( {9x{y^4} - 12{x^2}{y^3} + 6{x^3}{y^2}} \right):\left( { - 3x{y^2}} \right)\\ = 9x{y^4}:\left( { - 3x{y^2}} \right) - 12{x^2}{y^3}:\left( { - 3x{y^2}} \right) + 6{x^3}{y^2}:\left( { - 3x{y^2}} \right)\\ = - 3{y^2} + 4xy - 2{x^2}\end{array}\)
Không làm tính chia, hãy xét xem đa thức A có chia hết cho đơn thức B không.
\(A=15xy^2+17xy^3+18y^2\)
\(B=6y^2\)
Bài giải:
A chia hết cho B vì mỗi hạng tử của A đều chia hết cho B (mỗi hạng tử của A đều có chứa nhân tử y với số mũ lớn hơn hay bằng 2 bằng với số mũ của y trong B).
Ai đúng, ai sai ?
Khi giải bài tập: "Xét xem đa thức A = 5x4 – 4x3 + 6x2y có chia hết cho đơn thức B = 2x2 hay không ?".
Hà trả lời: "A không chia hết cho B vì 5 không chia hết cho 2".
Lời giải của bạn Hà sai, lời giải của bạn Quang đúng.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức 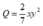 thì A=B.Q
thì A=B.Q
Do đó, đơn thức A chia hết cho đơn thức B.
Câu 4. Cho đơn thức A= 8x^4 và hai đơn thức B= 5x^3 và C= 2x^5 . Chọn khẳng định đúng:
A. Đơn thức A chia hết cho đơn thức B
B. Đơn thức A chia hết cho đơn thức
C. Đơn thức A không chia hết cho đơn thức
D. Đơn thức A chia hết cho cả đơn thức B và C
Câu 40. Hai cạnh kề của hình bình hành tỉ lệ với 1 và 2 và chu vi của hình bình hành bằng 13cm. Khi đó độ dài hai cạnh kề của hình bình hành là
A. 12cm và 18cm B. 5cm và 10cm
C. 15cm và 30cm D. 9cm và 18cm
Câu 39. Nếu hình bình hành ABCD có góc A = 530 thì
A.Góc D= 530 B. Góc B= Góc C = 530. C. Góc C= 1270 D. Góc D= 1270
Câu 37. Hãy chọn khẳng định sai?
A. Tứ giác có các cặp cạnh đối song song là hình bình hành.
B. Tứ giác có các góc đối bằng nhau là hình bình hành.
C. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
D. Hình thang có hai góc kề một đáy bằng nhau là hình bình hành.
Câu 36. Cho hình hình thang ABCD có AB//CD độ dài đường trung bình EF= 7cm và AB/CD=3/4 Khi đó độ dài hai đáy AB và CD lần lượt là
A. 6cm và 8cm. B. 8cm và 6cm.
C. 3cm và 4cm. D. 4cm và 3cm.
Câu 34: Cho tứ giác ABCD có góc A= 750,B= 1050 , C= 800Khi đó số đo của góc D bằng :
A. 100 0 B. 1050 C. 750 D. 800
Câu 32. Cho tứ giác ABCD có AB//CD và góc A= góc B , hãy chọn khẳng định đúng
A. Tứ giác ABCD là hình bình hành.
B. Tứ giác ABCD là hình thang cân.
C. Tứ giác ABCD là hình thang vuông.
D. Tứ giác ABCD có góc bằng nhau.
Câu 31. Khẳng định đúng là
A. Hình thang cân là tứ giác có hai cạnh đối song song.
B. Trong hình thang cân hai đường chéo bằng nhau.
C. Hình thang cân là tứ giác có hai góc bằng nhau.
D. Hình thang cân là tứ giác có hai góc đối bằng nhau.
Câu 30. Cho x + y = 2 và xy = 1 giá trị của biểu thức x3 + y3 bằng:
A . 8 B. 6 C. 4 D. 2
Không làm tính chia, hãy xét xem đa thức A có chia hết cho đơn thức B không:
A = 15xy2 + 17xy3 + 18y2
B = 6y2.
vì các hạng tử của đa thức A chia hết cho đơn thức B nên A chia hết cho B
A chia hết cho B vì mỗi hạng tử của A đều chia hết cho B (mỗi hạng tử của A đều có chứa nhân tử y với số mũ lớn hơn hay bằng 2 bằng với số mũ của y trong B).
Cho biểu thức \(A=\frac{-4ax^2y^5}{\left(b+1\right)^3}\)
Trong các trường hợp sau, trường hợp nào biểu thức A là đơn thức? Trong trường hợp đó hãy cho biết hệ số và bậc của đơn thức đối vs mỗi biến và đối vs tập hợp vs tập hợp các biến số
a) a,b là hằng
b) Chỉ có a là hằng
c) Chỉ có b là hằng
a) nếu a,b là hằng thì A là đơn thức
đơn thức A có hệ số \(\frac{-4a}{\left(b+1\right)^3}\); có bậc 2 đối với x, có bậc 5 đối với y và có bậc 7 đối với tập hợp các biến
b) Nếu chỉ có a là hằng thì A không phải đơn thức vì A có chứa phép chia, phép cộng đối với biến b
c) Nếu b là hằng thì A là đơn thức
Đơn thức A có hệ số là \(\frac{-4a}{\left(b+1\right)^3}\), có bậc 1 đối với a ; bậc 2 đối với x ; bậc 5 đối với y và có bậc 8 đối với tập hợp các biến
cho da thuc M=4x3y2-3x2y+xy2
a)Không làm tính chia ,hãy xét xem đa thức M có chia hết cho đơn thức 2xy khong
b)phân tích đa thức M thành nhân tử bằng cách đặt 2xy làm nhân từ chứng.Từ đó hãy chỉ ra thương trong phép chia đa thức M cho nhân tử chung đó