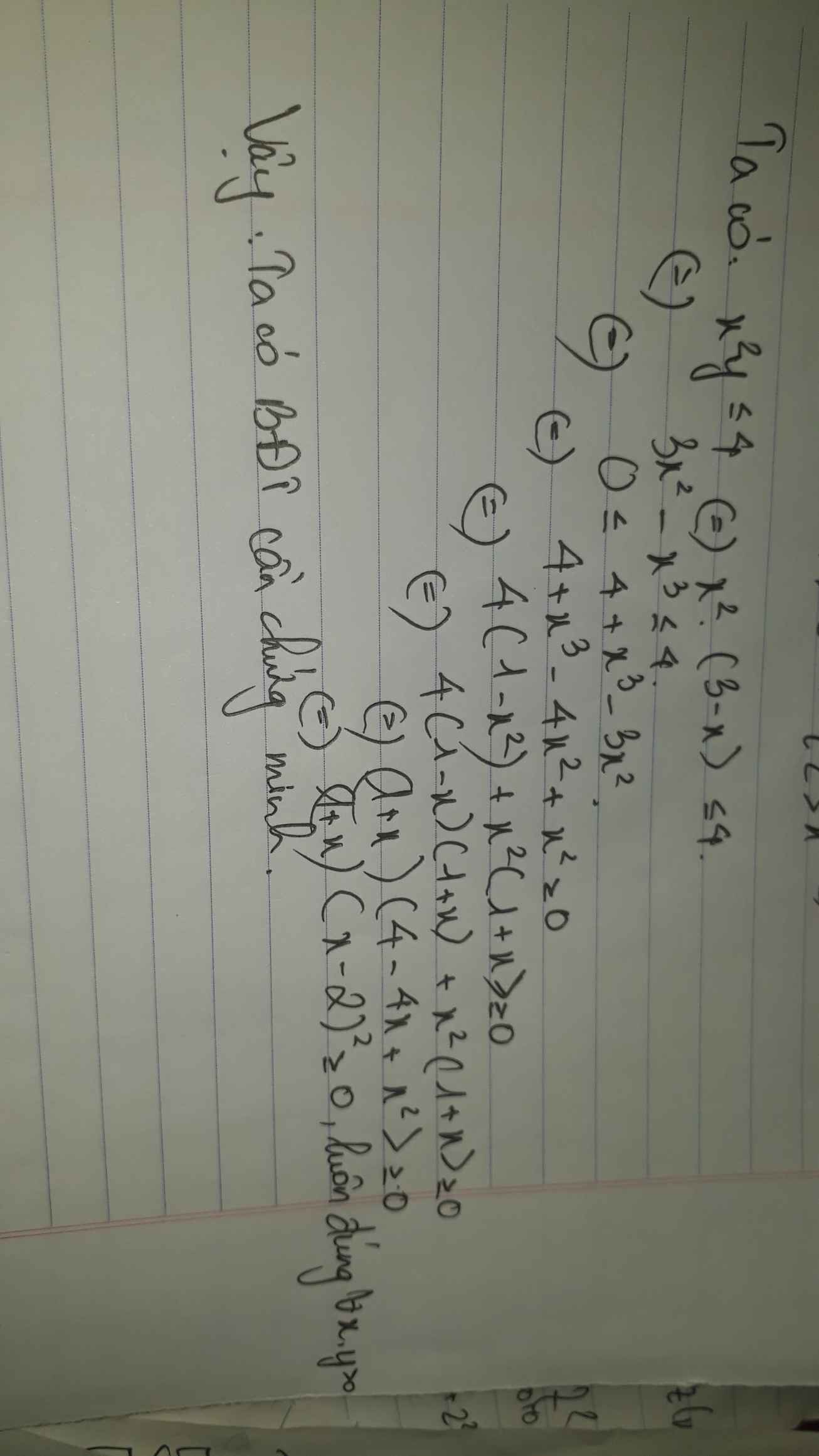Cho mình hỏi có phải HD đã sử dụng bđt vecto k ạ; nếu bđt vecto thì |vt a| + |vt b| >= |vt a + vt b|= căn [3^2 + (x+2+x-2)^2 +4^2 ] chứ ạ. Giải thích giúp mình với. Mình cảm ơn!!!

Những câu hỏi liên quan
Cho mình hỏi lúc làm bài liên quan đến BĐT Cô si dạng Engel ấy ạ, lúc áp dụng BĐT này thì ở trên có cần phải chứng minh không ạ?
xài bđt phụ mới cần phải chứng minh nhé
mà tau nhớ làm gì có Cô si dạng Engel ??? ._.
Ý mày là không tồn tại cái BĐT tên Cosi dạng engel á:")?
Cauchy-Schwarz dạng Engel thì có :)) còn Cauchy dạng Engel chưa nghe bao giờ ???
Xem thêm câu trả lời
cho mình hỏi có bđt nào có dạng: abc\(\le\left(\frac{a+b+c}{3}\right)^3\)không ạ?. mình từng thấy có bài áp dụng bđt này nma vẫn không biết nó là bđt phụ hay tên là gì. mình cảm ơn
\(abc\le\left(\frac{a+b+c}{3}\right)^3\Leftrightarrow\sqrt[3]{abc}\le\frac{a+b+c}{3}\)
BĐT Cô- si
đánh giá từ tbn sang tbc đấy bạn
Vào thi tuyển 10 có được sử dụng các dạng BĐT như BĐT Cô-si ko? (có cần phải chứng minh ko)
TL:
Chỗ tôi được phép sử dụng luôn ko cần chứng minh
HT
????
cho 1 vé báo cáo free nhé
là sao vậy?
Xem thêm câu trả lời
Cho mình hỏi bđt này có ấp dụng đc từ cosy hay kh ạ
(x + y +z )2 >= 3(ab+bc+ca)
Không được đâu em nhé! Em xem lại cái đề nhé!
bdt <=> \(x^2+y^2+z^2+2xy+2yz+2xz-3xy-3yz-3zx\ge0\)
<=> \(x^2+y^2+z^2-xy-yz-zx\ge0\)
<=> \(2x^2+2y^2+2z^2-2xy-2yz-2zx\ge0\)
<=> \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\) luôn đúng
vậy bđt ban đầu luôn đúng.
À vâng em cảm ơn ạ lúc đánh đề em ghi nhầm ạ
Bên mình là quận Thủ Đức sắp có cuộc thi chọn HSG thì mình muốn hỏi là khi đi thi có cần được dùng thẳng BĐT AM-GM 3 số không (hay còn gọi là BĐT Cô-Si 3 số) hay phải chứng minh :< có ai biết không ạ cảm ơn
chứng minh nó thì phải cm am-gm 2 số sau đó là 4 số @@ dài lắm
Đúng 0
Bình luận (0)

Sử dụng bđt am - gm ạ!

Sử dụng bđt am - gm ạ!
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(< =>\left(\dfrac{1}{a}+\dfrac{1}{b}\right).\left(a+b\right)\ge4\)
\(< =>1+\dfrac{b}{a}+\dfrac{a}{b}+1\ge4\)
\(< =>2+\dfrac{a}{b}+\dfrac{b}{a}\ge4\)(luôn đúng với mọi a,b là số thực dương)
Thật vậy có \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{a}{b}.\dfrac{b}{a}}=2\)(BĐT Cosi)
\(=>2+\dfrac{a}{b}+\dfrac{b}{a}\ge2+2=4\left(đpcm\right)\)
dấu"=" xảy ra<=>a=b
Đúng 1
Bình luận (0)
Em có cài nầy muốn hỏi mọi người ạ :
Bài toán : Cho \(x^2+y^2=52\). Tìm GTLN của \(A=2x+3y\)
Cho em hỏi là còn cách làm bài này ngoài cách sử dụng BĐT Bu - nhi - a - cốp - xki không ạ ?? Nếu có thì giúp em nha !
SIêu nhân henshin! kkk
\(102=x^2+y^2+52\)
\(=\left(x^2+16\right)+\left(y^2+36\right)\)
\(\ge8\left|x\right|+12\left|y\right|\ge8x+12y=4A\)
\(\Rightarrow A\le26\) tại x=4;y=6
Không chắc:v Nếu có thêm dấu giá trị tuyệt đối nữa thì ko dùng cosi được thì phải
zZz Cool Kid_new zZz Vậy à bạn , cảm ơn nhiều nhé!!
Cho a, b > 0. Chứng minh:
Hd : sử dụng BĐT Côsi cho hai số dương a, b và 1 + ab
Vì a>0; b>0 nên a + b \geq 4ab1+ab4ab1+ab
\Leftrightarrow (a + b)(1 + ab)\geq 4ab
\Leftrightarrow a + b + a^2b+ab^2\geq 4ab
\Leftrightarrow a + b + a^b + ab^2 - 4ab\geq 0
\Leftrightarrow (a^2b - 2ab + b) + (ab^2 - 2ab +a) \geq 0
\Leftrightarrow b(a^2 -2a + 1) + a(b^2 - 2B + 1)\geq 0
\Leftrightarrow b(a-1)^2 + a(b-1)^2\geq 0
\Rightarrow Bất đẳng thức đúng\Rightarrow đpcm.
Đúng 0
Bình luận (0)
Vì a,b > 0 =) ab > 0
Áp dụng BĐT Côsi cho hai số a,b không âm ta có :
\(\frac{a+b}{2}\ge\sqrt{ab}\)
\(\Rightarrow a+b\ge2\sqrt{ab}\)
Áp dụng BĐT Côsi cho hai số 1 , ab không âm ta có :
\(\frac{1+ab}{2}\ge\sqrt{ab}\)
\(\Rightarrow1+ab\ge2\sqrt{ab}\)
Ta có :
\(\frac{4ab}{1+ab}\le\frac{4ab}{2\sqrt{ab}}\)(Vì \(1+ab\ge2\sqrt{ab}\))
mà \(\frac{4ab}{2\sqrt{ab}}=2\sqrt{ab}\)
\(\Rightarrow\frac{4ab}{1+ab}\le2\sqrt{ab}\)(1)
Lại có : \(a+b\ge2\sqrt{ab}\)(2)
Từ (1) và (2) \(\Rightarrow a+b\ge\frac{4ab}{1+ab}\)
Chúc bạn học tốt =))![]()
Đúng 0
Bình luận (0)