cho hình bình hành ABCD có CD= 2AD; m là trung điểm của CD. Chứng minh:
a) AM là trung điểm của góc A
b) BM là trung điểm của góc B
c) góc ABM= 90 độ
Cho hình bình hành ABCD có AB=2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD. Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông.
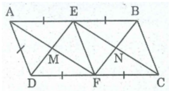
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = 1/2 DE (tính chất hình thoi)
MF = 1/2 AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ ∠ A = 90 0 ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ ∠ A = 90 0
Hình thoi AEFD có ∠ A = 90 0 nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.
cho hình bình hành ABCD có CD=2AD M là trung điểm cạnh CD khi đó góc AMD =???
Bài 3. Cho hình thang cân ABCD có AB // CD, CD =2AB =2AD. Lấy E là trung điểm CD.
Chứng minh ABED là hình bình hành.
Xét tứ giác ABED có
AB//ED
AB=ED
=>ABED là hbh
Vì `E` là trung điểm `CD` nên `CE = ED = AB = AD`.
Vì `AB //// CD => AB //// ED`.
Và `AB = ED => ABED` là hình bình hành.
Cho hình bình hành ABCD, có AB = 2AD. Gọi E, F theo thứtựcủa trung điểm AB, CD. a, Chứng minh rằng: Tứgiác AEFD, EBCF là hình thoi. b, M là giao điểm của AF và DE, N là giao điểm của CE và BE. Tứgiác MENF là hình gì? c, Chứng minh: MN // AB d, Chứng minh rằng: Các đường thẳng sau đồng quy : AC, BD, EF, MN
Cho hình bình hành ABCD có AB=2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD. Các tứ giác AEFD, AECF là hình gì? Vì sao?
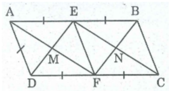
* Xét tứ giác AEFD, ta có:
AB // CD (gt) hay AE // FD
AE = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: AE = FD
Tứ giác AEFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
AD = AE = 1/2 AB . Vậy tứ giác AEFD là hình thoi.
* Xét tứ giác AECF, ta có: AE // CF (gt)
AE = 1/2 AB (gt)
CF = 1/2 CD (gt)
Suy ra: AE = CF
Tứ giác AECF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
Cho hình bình hành ABCD có AB = 2AD . Gọi E và F là trung điểm AB và CD
Các tứ giác AEFD và AECF là hình gì ?
+) Vì ABCD là hình bình hành
=> AB // CD và AB = CD
hay AE // DF và AE = DF
=> AEFD là hình bình hành
+) Vì ABCD là hình bình hành
=> AE // FC và AE = FC
=> AECF là hình bình hành
Ta có:
\(E\) là trung điểm của \(AB\left(gt\right)\) nên \(EA=EB=\frac{1}{2}AB\)
\(F\) là trung điểm của \(CD\left(gt\right)\) nên \(FC=FD=\frac{1}{2}CD\)
Mà \(AB=CD\) (cạnh đối hình bình hành \(ABCD\) )
nên \(EA=FD\) \(\left(1\right)\)
Vì \(AB\text{//CD}\) (theo tính chất cạnh đối hình bình hành \(ABCD\) ) nên \(EA\text{//FD}\) \(\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra, tứ giác \(AEFD\) là hình bình hành \(\left(3\right)\)
Lại có:
\(AB=2AD\left(gt\right)\Rightarrow AD=\frac{1}{2}AB\)
Do đó: \(EA=AD\left(=\frac{1}{2}AB\right)\) \(\left(4\right)\)
Từ \(\left(3\right);\left(4\right)\) suy ra, \(AEFD\) là hình thoi.
Cho hình bình hành ABCD có AB = 2AD. E là trung điểm AB, F là trung điểm CD. AF cắt ED tại I, BF cắt CE tại K.
a) AECF, AEFD, EIKF là hình gì? Chứng minh, giải thích
b) Tìm điều kiện của hình bình hành ABCD để EIKF là hình vuông
Cho hình bình hành ABCD có AB = 2AD và góc D. = 70 độ . Gọi H là hình. chiếu của B trên AD, M là trung điểm của CD. Tính góc HMC
cho hình bình hành abcd có ab = 2ad và A = 100độ .Gọi E, F theo thứ tự là trung điểm của các cạnh AB và CD . Tính Số Đo góc B
Cho hình bình hành ABCD có CD=2AD;N,M lần lượt là trung diểm các cạnh AB, CD
a) Tứ giác BMDN là hình gì? vì sao ?
b)Gọi giao điểm của BM,DN vs AC lần lượt là H,K. Chứng minh Ch = 1/3 AC
c) Tìm điều kiện của hình bình hành ABCD để BMDN là hình thoi