cho hai đa thức f(x) = 5x^2 - 3x +4; g(x) =5x^2 + x -2. Tim x để f(x) =g(x)

Những câu hỏi liên quan
Bài 1. Cho hai đa thứcf (x) -2x^4-3x^3+4x^4-x^2+5x+3x^2+5x^3+6 g (x) x^4-x^3+x^2-5x-x^3-2x^2+3a) Thu gọn và sắp xếp đa thức f (x) và g (x) theo lũy thừa giảm dần của biến; cho biết bậc, hệsố cao nhất, hệ số tự do của mỗi đa thức.b) Tìm các đa thức h (x) và k (x), biếth (x) f (x)+ g (x) k (x) f (x)-2g (x)-4x^2c) Tính giá trị của đa thức f (x) khi x là số nguyên, thỏa mãn k (x) 0.d) Tìm giá trị nhỏ nhất của đa thức h (x) CHỈ CẦN LÀM CÂU c,d THÔI, a,b ko cần phải làmBài 2. (2.0 điểm)a) Tìm tất cả c...
Đọc tiếp
Bài 1. Cho hai đa thức
f (x)= -2x^4-3x^3+4x^4-x^2+5x+3x^2+5x^3+6 g (x)= x^4-x^3+x^2-5x-x^3-2x^2+3
a) Thu gọn và sắp xếp đa thức f (x) và g (x) theo lũy thừa giảm dần của biến; cho biết bậc, hệ
số cao nhất, hệ số tự do của mỗi đa thức.
b) Tìm các đa thức h (x) và k (x), biết
h (x)= f (x)+ g (x) k (x)= f (x)-2g (x)-4x^2
c) Tính giá trị của đa thức f (x) khi x là số nguyên, thỏa mãn k (x)= 0.
d) Tìm giá trị nhỏ nhất của đa thức h (x) CHỈ CẦN LÀM CÂU c,d THÔI, a,b ko cần phải làm
Bài 2. (2.0 điểm)
a) Tìm tất cả các giá trị nguyên của biến x để biểu thức sau nhận
giá trị nguyên M= 9x+5/3x-1
1:
a: f(x)=2x^4+2x^3+2x^2+5x+6
g(x)=x^4-2x^3-x^2-5x+3
c: h(x)=2x^4+2x^3+2x^2+5x+6+x^4-2x^3-x^2-5x+3=3x^4+x^2+9
K(x)=f(x)-2g(x)-4x^2
=2x^4+2x^3+2x^2+5x+6-2x^4+4x^3+2x^2+10x-6-4x^2
=6x^3+15x
c: K(x)=0
=>6x^3+15x=0
=>3x(2x^2+5)=0
=>x=0
d: H(x)=3x^4+x^2+9>=9
Dấu = xảy ra khi x=0
Đúng 0
Bình luận (0)
Cho hai đa thức: f(x)= 5x^4+x^3-x+11+x^4-5x^3
g(x)2x^2+3x^4+9-4x^2-4x^3+2x^4-x
a) Thu gon và sắp xếp mỗi đa thức trên theo lũy thừa giảm dần của biến.
b) Tính h(x)=f(x)-g(x)
c) Chứng tỏ rằng đa thức h(x) không có nghiêm
a) Ta có: \(f\left(x\right)=5x^4+x^3-x+11+x^4-5x^3\)
\(=\left(5x^4+x^4\right)+\left(x^3-5x^3\right)-x+11\)
\(=6x^4-4x^3-x+11\)
Ta có: \(g\left(x\right)=2x^2+3x^4+9-4x^2-4x^3+2x^4-x\)
\(=\left(3x^4+2x^4\right)-4x^3+\left(2x^2-4x^2\right)-x+9\)
\(=5x^4-4x^3-2x^2-x+9\)
Đúng 0
Bình luận (0)
b) Ta có: h(x)=f(x)-g(x)
\(=6x^4-4x^3-x+11-5x^4+4x^3+2x^2+x-9\)
\(=x^4+2x^2+2\)
Đúng 0
Bình luận (0)
c) Ta có: \(x^4\ge0\forall x\)
\(2x^2\ge0\forall x\)
Do đó: \(x^4+2x^2\ge0\forall x\)
\(\Leftrightarrow x^4+2x^2+2\ge2>0\forall x\)
Vậy: Đa thức h(x) không có nghiệm(Đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hai đa thức f(x) = 2x^4+5x^3-x+8 và g(x) =x^4-x^2+3x+9. Tìm đa thức h(x) sao cho:
a)f(x) - h(x) = g(x).
b) h(x) - g(x) =f(x)
Ta có:\(f\left(x\right)-h\left(x\right)=g\left(x\right)\Leftrightarrow h\left(x\right)=f\left(x\right)-g\left(x\right)\)
\(\Leftrightarrow h\left(x\right)=\left(2x^4+5x^3-x+8\right)-\left(x^4-x^2+3x+9\right)\)
\(=2x^4+5x^3-x+8-x^4-x^2-3x-9\)
\(=x^4+5x^3+x^2-4x-1.\)
Vậy, đa thức cần tìm là: \(h\left(x\right)=x^4+5x^3+x^2-4x-1.\)
Ta có: \(h\left(x\right)-g\left(x\right)=f\left(x\right)\Leftrightarrow h\left(x\right)=f\left(x\right)+g\left(x\right)\)
\(\Leftrightarrow h\left(x\right)=\left(2x^4+5x^3-x+8\right)+\left(x^4-x^2+3x+9\right)\)
\(=2x^4+5x^3-x+8+x^4-x^2+3x+9\)
\(=3x^4+5x^3-x^2+2x+17\)
Vậy, đa thức cần tìm là:\(h\left(x\right)=3x^4+5x^3-x^2+2x+17.\)
Đúng 0
Bình luận (0)
cho hai đa thức F(x) = 6^2- 5x+8+3x-3x^2 + 3x^3 ; G(x) = 12x^2- 6 - 9x^2 + 3x^3
tìm x để F(x) =G(x)
F(x)=62+5x+8+3x-3x2+3x3
=(36+8)+(5x+3x)-3x2+3x3
=3x3-3x2+8x+44
G(x)=12x2-6-9x2+3x3
=3x3+(12x2-9x2)-6
=3x3+3x2-6
F(x)+G(x)=3x3-3x2+8x+44+3x3+3x2-6
=(3x3+3x3)+(-3x2+3x2)+8x+(44-6)
=6x3+8x+38
Đúng 1
Bình luận (0)
\(F\left(x\right)=G\left(x\right)\\ \Rightarrow6^2-5x+8+3x-3x^2+3x^3=12x^2-6-9x^2+3x^3\\ \Leftrightarrow-3x^2-2x+44=3x^2-6\\ \Leftrightarrow6x^2+2x-50=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1+\sqrt{301}}{6}\\x=\dfrac{-1-\sqrt{301}}{6}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Ta có : F(x)=G(x) suy ra: 3x^3 + 3x^2 - 2x + 8 = 3x^3+3x^2 -6
3x^3+ 3x^2 -2x +8 -3X^3- 3x^2+6=0
(3x^3-3x^3)+(3x^2-3x^2)-2x+(8+6)=0
-2x +14 =0
2x =14
x = 7
Đúng 1
Bình luận (0)
cho hai đa thức:
E(x) = 3x^2 - 8x^3 + 5x^4 - 2 + 3x
F(x) = -3x^2 + 2x + 7x^4 -x^2 + 8
a) sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng dần của biến
b) hãy tính: E(x) + F(x); E(x) - F(x); 3.E(x) 2F(x)
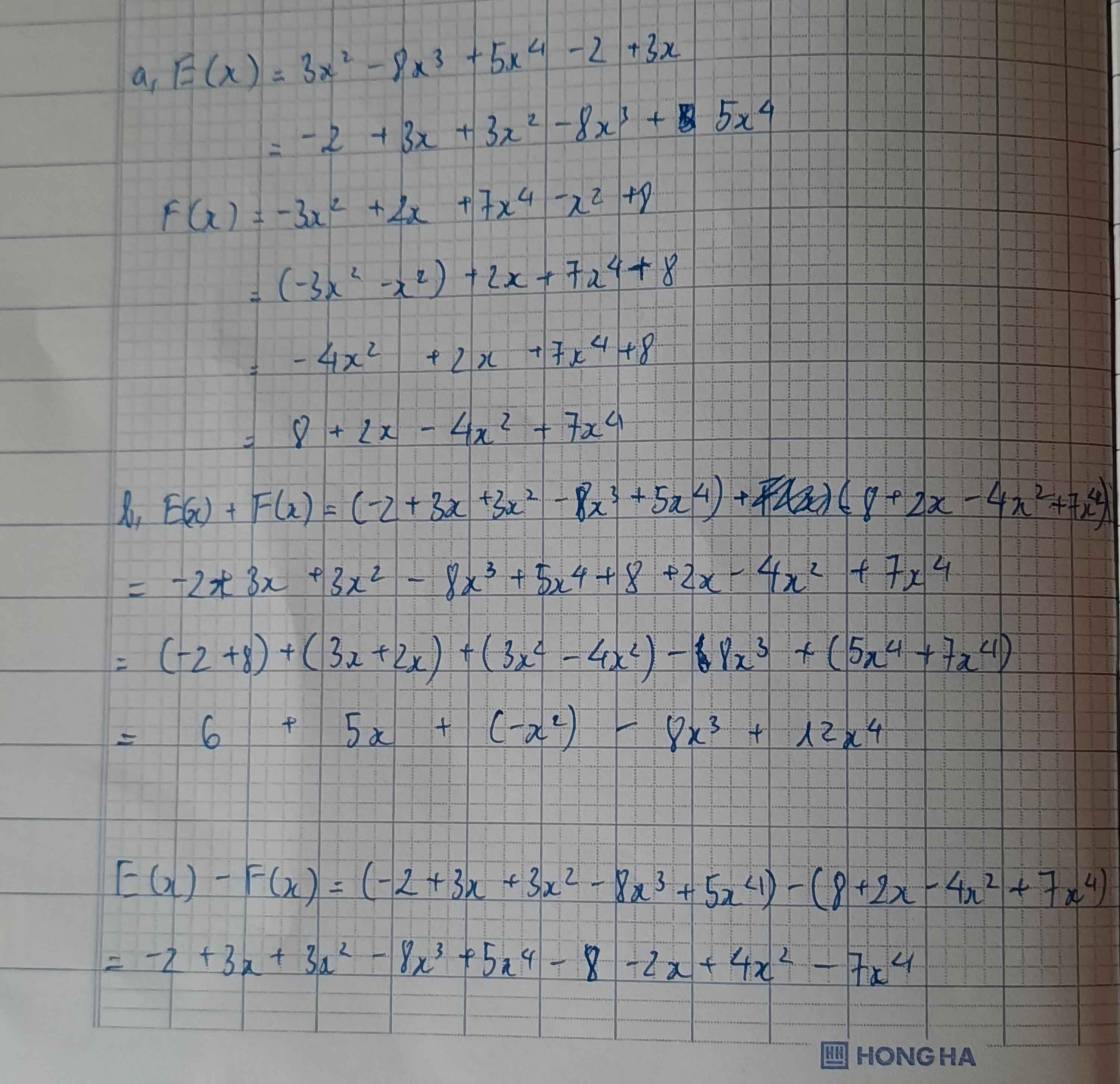
 *xl cậu nha ;-; câu cuối mình chưa học nên kbiet làm ;-;;;.
*xl cậu nha ;-; câu cuối mình chưa học nên kbiet làm ;-;;;.
Đúng 1
Bình luận (0)
Cho hai đa thức sau:
f(x)=3x4-5x3-x2+1007
g(x)=2x4+3x3+x-1007
a) Tính f(x)-g(x)-2014
b) Tìm đa thức h(x) sao cho 2014+g(x)-h(x)=f(x)
a)+)\(f\left(x\right)=3x^4-5x^3-x^2+1007\)
\(\Rightarrow f\left(x\right)=\left(3x^2-5x-1\right)x^2+1007\)
+)\(g\left(x\right)=2x^4+3x^3-1007\)
\(\Rightarrow g\left(x\right)=\left(2x^2+3x\right)x^2-1007\)
\(\Rightarrow f\left(x\right)-g\left(x\right)-2014=\left[\left(3x^2-5x-1\right)x^2+1007\right]-\left[\left(2x^2+3x\right)x^2-1007\right]-2014\)
\(f\left(x\right)-g\left(x\right)-2014=\left(3x^2-5x-1\right)x^2+1007-\left(2x^2+3x\right)x^2+1007-2014\)
\(f\left(x\right)-g\left(x\right)-2014=\left[\left(3x^2-5x-1\right)-\left(2x^2+3x\right)\right]x^2+\left(1007+1007-2014\right)\)
\(f\left(x\right)-g\left(x\right)-2014=3x^2-5x-1-2x^2-3x\)
\(\Rightarrow f\left(x\right)-g\left(x\right)-2014=x^2-2x-1=\left(x-1\right)^2\)
b)\(2014+g\left(x\right)-h\left(x\right)=f\left(x\right)\)
\(\Rightarrow-h\left(x\right)=f\left(x\right)-g\left(x\right)-2014\)
\(\Rightarrow-h\left(x\right)=\left(x-1\right)^2\)
\(\Rightarrow h\left(x\right)=-\left[\left(x-1\right)^2\right]\)
Chúc bạn học tốt
Bài 3 :
Cho đa thức :
f(x) = 9x^3 - 1/3x + 3x^2 - 3x + 1/3x^2 - 1/9x^3 - 3x^2 - 9x + 27 + 3x
a, Thu gọn đa thức f(x)
b, Tính f(3) , f(-3)
Bài 4
Cho đa thức :
F(x) = 2x^6 + 3x^2 + 5x^3 - 2x^2 + 4x^4 - x^3 + 1 - 4x^3 - x^4
a, Thu gọn đa thức f(x)
b, Tính f(1) , f(-1)
c, Chứng minh đa thức f(x) không có nghiệm
- Giúp mình với
Bài 3:
\(f\left(x\right)=9x^3-\frac{1}{3}x+3x^2-3x+\frac{1}{3}x^2-\frac{1}{9}x^3-3x^2-9x+27+3x\)
\(f\left(x\right)=\left(9x^3-\frac{1}{9}x^3\right)-\left(\frac{1}{3}x+3x+9x-3x\right)+\left(3x^2-3x^2\right)+27\)
\(f\left(x\right)=\frac{80}{9}x^3-\frac{28}{3}x+27\)
Thay x = 3 vào đa thức, ta có:
\(f\left(3\right)=\frac{80}{9}.3^3-\frac{28}{3}.3+27\)
\(f\left(3\right)=240-28+27=239\)
Vậy đa thức trên bằng 239 tại x = 3
Thay x = -3 vào đa thức. ta có:
\(f\left(-3\right)=\frac{80}{9}.\left(-3\right)^3-\frac{28}{3}.\left(-3\right)+27\)
\(f\left(-3\right)=-240+28+27=-185\)
Đúng 0
Bình luận (0)
Bài 4: \(f\left(x\right)=2x^6+3x^2+5x^3-2x^2+4x^4-x^3+1-4x^3-x^4\)
\(f\left(x\right)=2x^6+\left(3x^2-2x^2\right)+\left(5x^3-x^3-4x^3\right)+\left(4x^4-x^4\right)\)
\(f\left(x\right)=2x^6+x^2+3x^4\)
Thay x=1 vào đa thức, ta có:
\(f\left(1\right)=2.1^6+1^2+3.1^4=2+1+3=6\)
Đa thức trên bằng 6 tại x =1
Thay x = - 1 vào đa thức, ta có:
\(f\left(-1\right)=2.\left(-1\right)^6+\left(-1\right)^2+3.\left(-1\right)^4=2+1+3=6\)
Đa thức trên có nghiệm = 0
Đúng 0
Bình luận (0)
Cho hai đa thức
f
(
x
)
x
3
-
3
x
2
+
2
x
-
5
+
x
2
,
g
(
x
)
-
x
3
-
5
x
+
3
x...
Đọc tiếp
Cho hai đa thức
f ( x ) = x 3 - 3 x 2 + 2 x - 5 + x 2 , g ( x ) = - x 3 - 5 x + 3 x 2 + 3 x + 4 .
c. Tính nghiệm của f(x) + g(x)
c. Ta có f(x) + g(x)
=(x3 - 2x2 + 2x - 5) + (-x3 + 3x2 - 2x + 4) = x2 - 1
Ta có x2 - 1 = 0 ⇒ x2 = 1 ⇒ x = 1,x = -1
Vậy nghiệm của đa thức h(x) là x = ±1 (1 điểm)
Đúng 0
Bình luận (0)
tìm hai đa thức f(x) và g(x) thỏa mãn biểu thức sau
f(x)+g(x)= 2x^4+5x^2-3x^2
f(x)-g(x)=x^4-x^2+2x
f(x) + g(x) = 2x4 + 2x2
f(x) - g(x) = x4 - x2 + 2x
suy ra : f(x) = [ ( 2x4 + 2x2 ) + ( x4 - x2 + 2x ) ] : 2 = \(\frac{3x^4+x^2+2x}{2}\)
g(x) = [ ( 2x4 + 2x2 ) - ( x4 - x2 + 2x ) ] : 2 = \(\frac{x^4+3x^2-2x}{2}\)
Đúng 0
Bình luận (0)























