a/

\(\Rightarrow3=4m.2-m-5\Leftrightarrow m=\dfrac{8}{5}\)

b/

Tọa độ A là \(A\left(x_0;y_0\right)\)

\(\Rightarrow y_0=4mx_0-m-5\forall m\)

\(\Leftrightarrow\left(4x_0-1\right)m-\left(y_0+5\right)=0\forall m\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x_0-1=0\\y_0+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{4}\\y_0=-5\end{matrix}\right.\)

=> d1 luân đi qua điểm A cố định \(A\left(\dfrac{1}{4};-5\right)\forall m\)

Tọa độ B là \(B\left(x_1;y_1\right)\)

\(\Rightarrow y_1=\left(3m^2+1\right)x_1+m^2-4\forall m\)

\(\Leftrightarrow3m^2x_1+x_1+m^2-4-y_1=0\forall m\)

\(\Leftrightarrow\left(3x_1+1\right)m^2+x_1-y_1-4=0\forall m\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+1=0\\x_1-y_1-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{3}\\y_1=-\dfrac{13}{3}\end{matrix}\right.\)

=> d2 luân đi qua điểm B cố định \(B\left(-\dfrac{1}{3};-\dfrac{13}{3}\right)\)

d/ d1//d2 khi

\(\left\{{}\begin{matrix}4m=3m^2+1\\-m-5\ne m^2-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\\m^2+m+1\ne0\end{matrix}\right.\)

Ta có \(m^2+m+1>0\forall m\)

\(\Rightarrow\left[{}\begin{matrix}m_1=1\\m_2=\dfrac{1}{3}\end{matrix}\right.\)

e/

\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) tìm m để phương trình có nghiệm

Tìm giao

\(\Rightarrow4mx-\left(m+5\right)=\left(3m^2+1\right)x+m^2-4\) khi m=2

Thay m=2 tìm x rồi thay vào d1 hoặc d2 để tìm y

a: Vì M nằm trên d1 nên M(x;-x-2)

Theo đề, ta có: \(\dfrac{\left|x\cdot1-3\cdot\left(-x-2\right)+1\right|}{\sqrt{1^2+\left(-3\right)^2}}=3\)

\(\Leftrightarrow\left|x+3x+6+1\right|=3\sqrt{10}\)

\(\Leftrightarrow\left|4x+7\right|=3\sqrt{10}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3\sqrt{10}-7}{4}\\x=\dfrac{-3\sqrt{10}-7}{4}\end{matrix}\right.\)

a: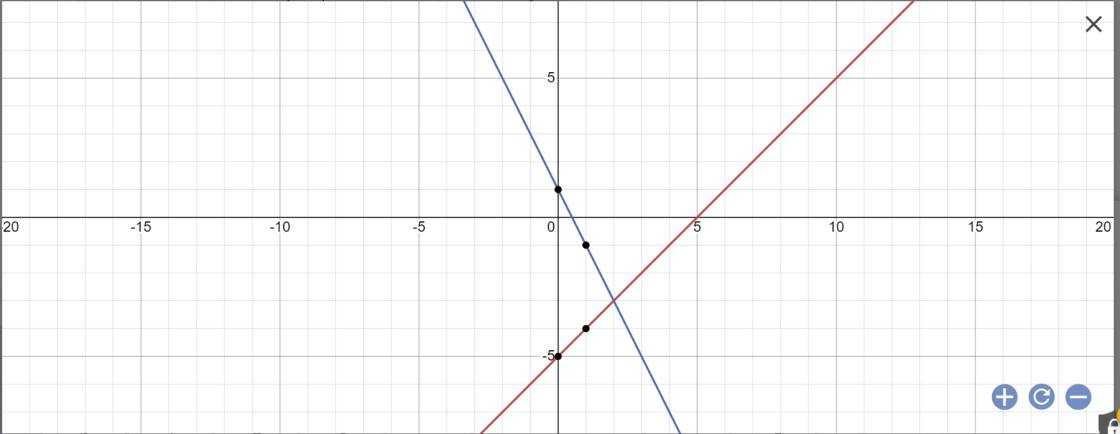 

b: Phương trình hoành độ giao điểm là:

-2x+1=x-5

=>-2x-x=-5-1

=>-3x=-6

=>x=2

Thay x=2 vào y=x-5, ta được:

\(y=2-5=-3\)

Vậy: (d1) cắt (d2) tại A(2;-3)

c: (d1): y=x-5

=>x-y-5=0

Khoảng cách từ O(0;0) đến (d1) là:

\(d\left(O;\left(d1\right)\right)=\dfrac{\left|0\cdot1+0\cdot\left(-1\right)-5\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{\sqrt{2}}\)

(d2): y=-2x+1

=>y+2x-1=0

=>2x+y-1=0

Khoảng cách từ O đến (d2) là:

\(d\left(O;\left(d2\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)

M thuộc (d1) nên M(1-2t;1+t)

Theo đề, ta có: d(M;d2)=d(M;d3)

=>\(\dfrac{\left|\left(1-2t\right)\cdot3+\left(1+t\right)\cdot4-4\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|\left(1-2t\right)\cdot4+\left(1+t\right)\cdot\left(-3\right)+2\right|}{\sqrt{4^2+\left(-3\right)^2}}\)

=>|-6t+3+4t+4-4|=|4-8t-3t-3+2|

=>|-2t+3|=|-11t+3|

=>-2t+3=-11t+3 hoặc -2t+3=11t-3

=>t=0 hoặc t=6/13

=>M(1;1); M(1/13; 19/13)

Đáp án D

a) Để (d1)//(d2) thì 

\(\left\{{}\begin{matrix}2m=1\\-m^2+4\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\-m^2\ne-2\end{matrix}\right.\Leftrightarrow m=\dfrac{1}{2}\)

b) Chắc là tìm khoảng cách giữa hai đường thẳng khi chúng song song

Tại \(m=\dfrac{1}{2}\Rightarrow y=x+\dfrac{15}{4}\)

Chọn \(A\left(0;2\right)\in\left(d_1\right)\)

Khi đó khoảng cách giữa hai đường thẳng là khoảng cách từ điểm A đến đường thẳng \(\left(d_2\right)\)

Gọi đường thẳng \(\Delta\) vuông góc với \(\left(d_2\right)\) và đi qua A có dạng: \(\Delta:y=-x+c\)

\(A\in\Delta\Rightarrow2=c\)

\(\Rightarrow\Delta:y=-x+2\)

Gọi giao điểm của \(\Delta\) và \(d_2\) là H

Tọa độ giao điểm của H là nghiệm của hệ:\(\left\{{}\begin{matrix}y=x+\dfrac{15}{4}\\y=-x+2\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{7}{8}\\y=\dfrac{23}{8}\end{matrix}\right.\)\(\Rightarrow H\left(-\dfrac{7}{8};\dfrac{23}{8}\right)\)

Khoảng cách giữa hai đường thẳng bằng độ dài đoạn AH

\(AH=\sqrt{\left(-\dfrac{7}{8}-0\right)^2+\left(\dfrac{23}{8}-2\right)^2}=\dfrac{7\sqrt{2}}{8}\)

Vậy...