Cho hình thang ABCD, có AB//CD. GỌi M; N lần lượt là trung điểm của AD và Bc. Biết MN= 28 cm và AB:CD= 3:5. tính độ dài AB và CD

Những câu hỏi liên quan
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD. Hình thang ABCD có thêm điều kiện gì thì MNPQ là hình vuông?
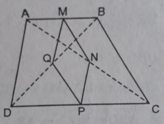
Hình thang ABCD là hình thang cân có hai góc kề một đáy đều bằng 45 0 thì MNPQ là hình vuông.
Đúng 0
Bình luận (0)
Trong không gian cho hình thang cân ABCD có AB//CD, AB a,CD 2a,AD a Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
Đọc tiếp
Trong không gian cho hình thang cân ABCD có AB//CD, AB = a,CD = 2a,AD = a Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
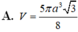
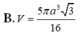
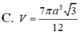
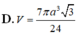
Trong không gian cho hình thang cân ABCD có AB//CD, ABa, CD2a, ADa. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K. A.
V
5
πa
3
3
8
B.
V
5
πa
3...
Đọc tiếp
Trong không gian cho hình thang cân ABCD có AB//CD, AB=a, CD=2a, AD=a. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
A. V = 5 πa 3 3 8
B. V = 5 πa 3 3 16
C. V = 7 πa 3 3 12
D. V = 7 πa 3 3 12
Trong không gian, cho hình thang cân ABCD có AB//CD, AB a, CD 2a, AD a. Gọi M, N lần lượt là trung điểm của AB, CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thang ABCD quanh trục MN. Tính diệc tích xung quanh
S
x
q
của khối K A.
S
x
q
πa
2
2
B. ...
Đọc tiếp
Trong không gian, cho hình thang cân ABCD có AB//CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB, CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thang ABCD quanh trục MN. Tính diệc tích xung quanh S x q của khối K
A. S x q = πa 2 2
B. S x q = 3 πa 2 2
C. S x q = 3 πa 2
D. S x q = πa 2
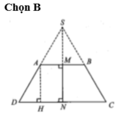
Gọi S là giao điểm của AD và BC. Nếu quay tam giác SCD quanh trục SN, các đoạn thẳng SC. SB lần lượt tạo ra mặt xung quanh của hình nón ( H 1 ) v à ( H 2 ) .
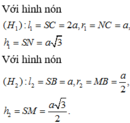
Đúng 0
Bình luận (0)
1) cho hình thang ABCD có AB//CD;AB>CD;AC vuông góc với BD.Trên cạnh đáy AB lấy điểm M sao cho AM bằng độ dài đường trung bình của hình thang ABCD .CM:AC là tia phân giác góc A
2)Cho hình thang ABCD có góc A=góc B=90 độ ;BC=2AD=2AB .Gọi M là 1 điểm trên đáy nhỏ AB kẻ Mx vuông với MB .Mx cắt CD tại N.CM:MB=MN
Bài 1: Cho hình thang ABCD ( có AB// CD). Gọi E là trung điểm của AD. Kẻ đường thẳng qua E song song với AB và cắt BC tại F.
a) Chứng minh F là trung điểm của BC.
b) Cho AB = 4; CD =12. Tính EF.
Bài 2: Cho hình thang ABCD (có AB // CD; AB < CD). Gọi E, F, G lần lượt là trung điểm của AD, AC, BD.
a) Chứng minh E, F, G thẳng hàng.
b) Chứng minh EF = (CD-AB)/2.
Bài 1: Cho hình thang ABCD ( có AB// CD). Gọi E là trung điểm của AD. Kẻ đường thẳng qua E song song với AB và cắt BC tại F.
a) Chứng minh F là trung điểm của BC.
b) Cho AB = 4; CD =12. Tính EF.
Bài 2: Cho hình thang ABCD (có AB // CD; AB < CD). Gọi E, F, G lần lượt là trung điểm của AD, AC, BD.
a) Chứng minh E, F, G thẳng hàng.
b) Chứng minh EF = (CD-AB)/2.
1.Cho tứ giác ABCD, có AB=CD. Gọi P,Q là trung điểm AC, BD. C/m đường thẳng PQ taoh bởi AB và CD các góc bằng nhau
2. Cho tứ giác ABCD ( AB<CD) Gọi trung điểm 2 đường chéo BD,AC là E,F. C/m
a.Nếu ABCD là hình thang có đáy AB,VD thì EF=CD-AB/2
b, Nếu EF= CD-AB/2 thì ABCD là hình thang
Mong các bạn giúp đỡ , mình ko làm đc. Cảm ơn mọi người nhiều!
Cho hình thang ABCD, có AB // CD và AB < CD. Gọi M là giao điểm của AD và BC. Gọi H, E, F, G lần lượt là trung điểm của AM, BM, AC, BD. Chứng minh HEFG là hình thang.
Cho hình thang ABCD có A=D=90 độ và 2 đường chéo vuông góc với nhau. Gọi AB=m, CD=n. Tìm diện tích bé nhất của hình thang ABCD
Diện tích hình thang này là 1 hằng số \(S=\dfrac{1}{2}\left(m+n\right)\sqrt{mn}\) nên không thể có giá trị lớn nhất hay nhỏ nhất gì đó được
Đúng 1
Bình luận (3)









