Bạn chỉ cần áp dụng hệ thức lượng là đc rồi o0o

Cho tam giác ABC vuông tại A , đường cao AH . Chứng minh rằng 1/AH^2=1/AB^2+1/ac^2

2:

a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có

góc HAB=góc HCA

=>ΔHAB đồng dạng với ΔHCA

=>HA/HC=HB/HA

=>HA^2=HB*HC

b: BC=4+9=13cm

AH=căn 4*9=6cm

S ABC=1/2*6*13=39cm²

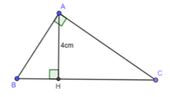
Ta có: H B H C = 1 4 ⇒ HC = 4HB

Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:

A H 2 = B H . C H ⇔ 4 2 = 4 B H 2 ⇔ B H = 2 ( c m ) ⇒ C H = 8 ( c m )

Ta có: BC = BH + HC = 2 + 8 = 10 (cm)

Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:

⇒ A B 2 = B H . B C ⇔ A B 2 = 2 . 10 ⇔ A B = 20 = 2 5 ( c m )

Áp dụng định lý Pitago cho ABH vuông tại A có: A B 2 + A C 2 = B C 2

⇔ 20 + A C 2 = 100 ⇔ A C 2 = 80 ⇒ A C = 80 = 4 5 ( c m )

Vậy chu vi tam giác ABC là: 4 5 + 2 5 + 10 = 6 5 + 10 c m

Đáp án cần chọn là: D

\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)

BC=HB+HC=6,25(cm)

AM=BC/2=3,125(cm)

\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)

\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)

+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :

\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)

+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\) 

\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\) 

\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)

+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :

\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)

\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)

+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :

\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)

AB=căn AH*AC=6(cm)

BC=căn AC^2-AB^2=căn 9^2-6^2=căn 45=3*căn 5(cm)

Xét ΔABC vuông tại B có sin C=AB/AC=6/9=2/3

nên góc C=42 độ

=>góc A=48 độ

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!

rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

viet ba dao nhu the co ma lam dc!!! 

a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)

AH=4*3/5=2,4cm

b: ΔCAD cân tại C

mà CH là đường cao

nên CH là phân giác của góc ACD

Xét ΔCAB và ΔCDB có

CA=CD

góc ACB=góc DCB

CB chung

Do dó: ΔCAB=ΔCDB

=>góc CDB=90 độ

=>BD là tiếp tuyến của (C)

tự vẽ hình 

ta có <HBA+<BAH= 90\(^0\)(vì tam giác ABH vg tại H)

Có <BAH+ <HAC= 90\(^0\)(vì tam giác ABC vg tại A)

=> <HBA=<HAC 

Xét tam giác BAH và ACH

<BHA=<AHC\(\left(90^0\right)\)

<ABH=<HAC

=> Tam giác BAH đồng dạng với tam giác ACH

=> BH/AH=AH/CH=> AH^2= BH*CH=4*9=36 cm 

b, ta có BC=BH+CH=4+9=13 cm 

S(ABC) = AH*BC=36*13=468 cm\(^2\)

 BÀI 1:

a)

·         Trong ∆ ABC, có:     AB²= BC.BH

                           Hay BC= =

·         Xét ∆ ABC vuông tại A, có:

    AB²= BH²+AH²

↔AH²= AB² – BH²

↔AH= =4 (cm)

b)

·         Ta có: HC=BC-BH

      àHC= 8.3 - 3= 5.3 (cm)

·         Trong ∆ AHC, có:    

·                                         

Bài 1:

a)  Áp dụng hệ thức lượng ta có:

   \(AB^2=BH.BC\)

\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)

\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)

Áp dụng Pytago ta có:

     \(AH^2+BH^2=AB^2\)

\(\Rightarrow\)\(AH^2=AB^2-BH^2\)

\(\Rightarrow\)\(AH^2=5^2-3^2=16\)

\(\Rightarrow\)\(AH=4\)

b)  \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)

Áp dụng hệ thức lượng ta có:

   \(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)

\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)

\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)

\(\Rightarrow\)\(HE=\frac{16}{5}\)

- Bạn ơi D ở đâu thế?