Cho hình thang ABCD có góc A và góc D là vuông góc. AB = 36 cm ; DC = 45 cm ; AD =40 cm . Trên AD lấy DM = 10 cm , từ M là đường cao thẳng song song có DC cắt BC tại N . Tính S hình thang ABNM.

Những câu hỏi liên quan
Cho hình thang ABCD có góc A và góc D vuông , có cạnh AB = 36 cm ,cạnh DC = 45cm , cạnh AD = 40 cm . Trên cạnh AD lấy đoạn DM =10cm , từ M kẻ đường thẳng song song với DC và cắt BC tại N . Tính diện tích hình thang ABCD
Diện tích hình thang abcd là
(45+36)×40:2=1620(cm2)
Chiều cao của hình tam giác ABC là
40-10=30(cm)
Diện tình hình tam giác ABN là
36×30:2=540(cm2)
Diện tích hình tam giác ncd là
45×10:2=225(cm2)
Diện tích hình tam giác and là
1620-(540+225)=855(cm)
Đáy lớn của hình thang abnm là
855×2:40=42,75(cm)
Diện tích hình thang abnm là
(36+42,75)×30:2=1181,25(cm2)
ĐS:1181,25cm2
Đúng 0
Bình luận (0)
Diện tích hình thang abcd là
(45+36)×40:2=1620(cm2)
Chiều cao của hình tam giác ABC là
40-10=30(cm)
Diện tình hình tam giác ABN là
36×30:2=540(cm2)
Diện tích hình tam giác ncd là
45×10:2=225(cm2)
Diện tích hình tam giác and là
1620-(540+225)=855(cm)
Đáy lớn của hình thang abnm là
855×2:40=42,75(cm)
Diện tích hình thang abnm là
(36+42,75)×30:2=1181,25(cm2)
ĐS:1181,25cm2
Đúng 0
Bình luận (0)
1, Cho hình thang ABCD ( AB // CD ) có góc B - góc C = 24° , góc A = 1,5 góc D . Tính các góc của hình thang .
2. Cho hình thang vuông ABCD ( góc A = góc D = 90°) đường chéo BD vuông góc với cạnh bên BC và BD = BC :
a, Tính các góc của hình thang .
b, Biết AB = 3 cm , Tính độ dài các cạnh BC,CD .
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)
Đúng 0
Bình luận (1)
cho hình thang abcd có góc a và góc d vuông , có cạnh ab = 36 cm , cạnh dc = 45 cm , cạnh ad =40 cm . trên cạnh ad lấy đoạn dm = 10 cm , từ m kẻ đường thẳng song song với dc và cắt bc tại n . tính diện tích hình thang abnm
Theo bài ra Cạnh AD=40cm, DM=10cm, nên AM = 40 - 10 = 30(cm); do đó AM = 3/4 AD hay AM = 3x MD. Từ M kẻ đường thẳng song song với DC và cắt BC tại N ( đối với HSTH có thể "chấp nhận" BN = 3/4 BC = 3x NC); hoặc các em có thể chứng tỏ như sau: S(BMN) = 3x S(NMC) ( Vì hai tam giác có chung đáy MN và đường cao hạ từ B xuống MN = 3 lần đường cao hạ từ C xuống MN...)
Từ đó ta có: NC = 1/3 BN ; hay BN = 3/4 BC.
S(ABCD); S(ABM); S(MCD) tính được
S(BMC) = S(ABCD) - S(ABM) - S(MCD)
Mà S(BMN) = 3/4 S(BMC)..... nên cũng tính được....từ đó tính được S(ABNM).
Đúng 0
Bình luận (0)
Diện tích tứ giác ABCD là : (50+60) x (40+10) : 2 = 2750 (cm2)
Diện tích tam giác BMC là : 2750 - 50 x 40 : 2 - 60 x 10 : 2 = 1450 (cm2)
Xét tam giác BMN và NMC có chung đỉnh M, đáy BN = NC x 4 => S_BMN = S_NMC x 4
Vậy diện tích BMN là : 1450 : (1 + 4) x 4 = 1160 (cm2)
Vậy diện tích hình thang ABNM là : 50 x 40 : 2 + 1160 = 2160 (cm2)
Đúng 1
Bình luận (0)
Diện tích tứ giác ABCD là : (50+60) x (40+10) : 2 = 2750 (cm2)
Diện tích tam giác BMC là : 2750 - 50 x 40 : 2 - 60 x 10 : 2 = 1450 (cm2)
Xét tam giác BMN và NMC có chung đỉnh M, đáy BN = NC x 4 => S_BMN = S_NMC x 4
Vậy diện tích BMN là : 1450 : (1 + 4) x 4 = 1160 (cm2)
Vậy diện tích hình thang ABNM là : 50 x 40 : 2 + 1160 = 2160 (cm2)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho hình thang ABCD có góc A và góc D vuông góc , AB bắn 50 cm, CD bằng 60 cm, AM bằng 40 cm và DM bằng 10 cm. Tính diện tích hình thang ABNM, biết NM song song với AB.
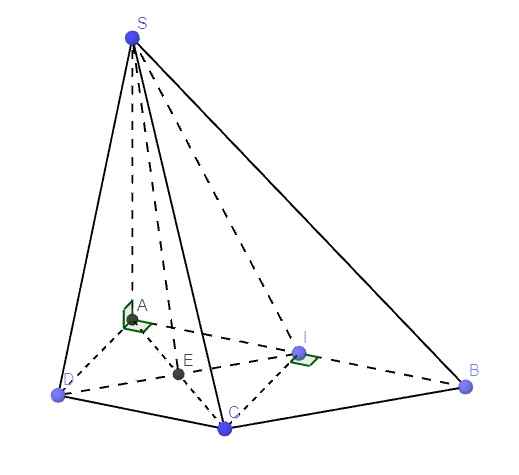
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB. SA vuông góc với (ABCD) a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
c.
Từ câu b ta có AICD là hình vuông \(\Rightarrow CI\perp AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CI\)
\(\Rightarrow CI\perp\left(SAB\right)\)
Lại có \(CI\in\left(SCI\right)\Rightarrow\left(SCI\right)\perp\left(SAB\right)\)
d.
I là trung điểm AB \(\Rightarrow CI\) là trung tuyến ứng với AB
Lại có \(CI=AD=a\) (AICD là hình vuông) \(\Rightarrow CI=\dfrac{1}{2}AB\)
\(\Rightarrow\Delta ACB\) vuông tại C
\(\Rightarrow BC\perp AC\) (1)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAC\right)\)
\(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAC\right)\)
Đúng 2
Bình luận (0)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
cho hình thang abcd có góc a và d vuông ,có ab là 36 cm , dc là 45 cm; ad là 40 cm .trên ad lấy dm là 10 cm. từ m kẻ đường thẳng song song với dc và cắt bc tại n. tính diện tích hình thang abnm ?
Cho hình thang vuông ABCD có góc A=góc D=90 độ,AB=AD=1/2DC
a)Tính các góc của hình thang
b)CM AC vuông góc CD
c)Tính chu vi hình thang nếu AB=3cm
(vẽ hình hộ)
a: Kẻ BH vuông góc CD
Xét tứ giác ABHD có
góc BAD=góc ADH=góc BHD=90 độ
AB=AD
=>ABHD là hình vuông
=>BH=HD=AB=DC/2
=>góc BDH=45 độ
DH=DC/2
=>H là trung điểm của DC
Xét ΔBDC có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBDC cân tại B
=>góc C=45 độ
=>góc ABC=135 độ
c: DC=2*3=6cm
AD=AB=3cm
BC=căn 3^2+3^2=3*căn 2cm
C=6+3+3+3căn 2=12+3căn 2(cm)
Đúng 1
Bình luận (0)