Xét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC nên MN là đường trung bình của hình thang:

Suy ra: MN// AB// CD và

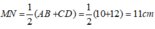
Suy ra: tứ giác MNCD là hình thang.

Vì M là trung điểm của AD và đường cao AH = 6cm nên chiều cao xuất phát từA của hình thang MNCD là:

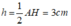
Diện tích hình thang ABNM là :

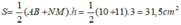
Chọn đáp án D

B

B 5.cm

B

hình như bạn cho cái đề thiếu BC nhỉ!

Cho tứ giác ABCD. Gọi M, N là trung điểm của AD và BC, biết MN =(AB + CD)/2. C/M ABCD là hình thang

gọi I là giao điểm của MN và BD 
ta có 
MN=(AB + DC)/2 
=> MI + IN = AB/2 + DC/2 
=> MI = AB/2 và IN = DC/2 
=> MI và IN là đường tb của tam giác ABD và tam giác BDC 
=> MI // AB và IN // DC 
vì M,I,N thẳng hàng nên => AB // DC => tứ giác ABCD là hình thang 

Cho mình hỏi sao MI=AB/2 và IN=DC/2

a) Xét hình thang ABCD(AB//CD) có 

M là trung điểm của AD(gt)

N là trung điểm của BC(gt)

Do đó: MN là đường trung bình của hình thang ABCD(Định nghĩa đường trung bình của hình thang)

Suy ra: MN//AB//DC và \(MN=\dfrac{AB+CD}{2}\)(Định lí 4 về đường trung bình của hình thang)

hay \(MN=\dfrac{3+5}{2}=\dfrac{8}{2}=4\left(cm\right)\)

b) Ta có: AD//BE(gt)

AD\(\perp\)DC(gt)

Do đó: BE\(\perp\)DC(Định lí 2 từ vuông góc tới song song)

Xét tứ giác ABED có 

\(\widehat{BAD}=90^0\)(gt)

\(\widehat{ADE}=90^0\)(gt)

\(\widehat{BED}=90^0\)(cmt)

Do đó: ABED là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

tau méch cô hoài nhá

a) Xét tam giác ABD có :

 M là trung điểm của AB

 F là trung điểm của BD

=) MF là đường trung bình của tam giác ABD

=) MF//AD và MF=\(\frac{1}{2}\)AD    (1)

Xét tam giác tam giác ACD có :

 N là trung điểm CD

 E là trung điểm AC

=) NE là đường trung bình của tam giác ACD

=) NE//AD và NE=\(\frac{1}{2}\)AD     (2)

Từ (1) và (2) =) Tứ giác MENF là hình bình hành