Cho hình thang ABCD(AB//CD) có AD=4cm; BC=6cm. các cạnh bên kéo dài cắt nhau tại M. nếu độ dài đoạn MA= 6cm thì đoạn MB bằng bao nhiêu cm?

Những câu hỏi liên quan
Cho hình thang ABCD (AB // CD) có đường cao AH = 4cm, AD = 5cm, BC = √80cm, CD = 20cm. Tính chu vi và diện tích hình thang ABCD.
ta có tam giác ADH vuông tại H
=> AH^2+HD^2=AD^2
=>HD^2=AD^2-AH^2
=5^2-4^2
=9
=>HD=3 cm
kẻ BK vuông góc với CD
=>ABKH là hình chữ nhật
=>AH=BK=4cm
tam giác BKC vuông tại K
=>BK^2+KC^2=BC^2
=>KC^2=BC^2-BK^2
=80-16
=64
=>KC=8 (cm)
lại có DH+HK+KC=20
=>HK=20-3-8=9 (cm)
=>AB+HK=9 cm
ta có chu vi hình thang ABCD là AB+BC+CD+DA=9+√80+20+5=34+√80(cm)
Cho hình thang cân abcd có đáy Ab=3cm đáy cd=5cm và cạnh bên aD=4cm tính chu vi hình thang cân abcd?
Chu vi hình thang cân là:
3+5+4+4=16(cm)
Đ/S:...
Đúng 1
Bình luận (0)
Vì ABCD là hình thang cân
=> AD = BC = 4cm
Chu vi hình thang cân ABCD là : 3+4+5+4=16 (cm)
Đúng 1
Bình luận (0)
Giải
Chu vi hình thang cân là :
3 + 5 + 4 + 4 = 16 ( cm )
Đáp số : 16 cm
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB//CD) có AB = AD = 1/2 CD. Tính SABCD biết AB = 2,5cm và BD = 4cm
Cho hình thang cân ABCD (AB//CD) biết AB=4cm,CD=10cm,AD=5cm.Tính diện tích hình thang
Cho hình thang ABCD có đáy AB và CD, biết AB=4cm, CD=8cm, BC=5cm ,AD=3cm. CM : ABCD là hình thang vuông
GIÚP TỚ VỚI !!! MAI NỘP RỒI
Kẻ BH//AD(H∈CD)BH//AD(H∈CD), kẻ BD
Ta có:
+) AB//CD (hình thang ABCD)
⇒B2ˆ=D1ˆ⇒B2^=D1^ ( 2 góc so le trong )
+) BH//AD (cách vẽ)
⇒D2ˆ=B1ˆ⇒D2^=B1^ ( 2 góc so le trong)
Xét ΔDABΔDAB và ΔBHDΔBHD, ta có:
B2ˆ=D1ˆ(cmt)B2^=D1^(cmt)
BD : chung
D2ˆ=B1ˆ(cmt)D2^=B1^(cmt)
⇒⇒ ΔDABΔDAB = ΔBHDΔBHD (gcg)
⇒AD=BH⇒AD=BH
mà AD=3cm(gt)AD=3cm(gt)
⇒BH=3cm⇒BH=3cm
+) ΔDABΔDAB = ΔBHDΔBHD (cmt)
⇒AB=DH⇒AB=DH
mà AB=4cm(gt)AB=4cm(gt)
⇒DH=4cm⇒DH=4cm
+) DH+HC=DC(H∈DC)DH+HC=DC(H∈DC)
⇒4+HC=8⇒4+HC=8
⇒HC=4cm⇒HC=4cm
Xét ΔBHC,ΔBHC, ta có:
52=32+4252=32+42
⇒BC2=BH2+HC2⇒BC2=BH2+HC2 (Định lý Py-ta-go)
⇒ΔBHC⇒ΔBHC vuông tại H
⇒H1ˆ=900⇒H1^=900
+) AD//BH
⇒ADHˆ=H1ˆ⇒ADH^=H1^ (2 góc động vị)
⇒ADHˆ=900⇒ADH^=900
⇒⇒ Hình thang ABCD là hình thang vuông
Bạn ơi 900 là 90 độ nha
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Cho hình thang cân ABCD,AB//CD.Biết AB=4cm,CD=10cm,AD=5cm.Tính S hình thang
Dựng hình thang cân ABCD có AB // CD, biết AD = 2cm, CD = 4cm, AC = 3,5cm
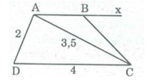
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán. Tam giác ADC dựng được vì biết ba cạnh AD = 2cm, CD = 4cm, AC= 3,5cm. Điểm B thỏa mãn 2 điều kiện:
- B nằm trên đường thẳng đi qua A và song song với CD.
- B cách D một khoảng bằng 3,5cm( vì ABCD là hình thang cân nên hai đường chéo bằng nhau).
Cách dựng:
- Dựng ∆ ADC biết:
AD = 2cm, AC = 3,5cm, CD = 4cm.
- Dựng tia Ax // CD. Ax nằm trong nửa mặt phẳng bờ AD chứa điểm C.
- Dựng cung tròn tâm D bán kính 3,5cm. Cung này cắt Ax tại B. Nối CB, ta có hình thang ABCD cần dựng.
Chứng minh:
Tứ giác ABCD là hình thang vì AB //CD.
AC = BD = 3,5cm
Vậy hình thang ABCD là hình thang cân.
Hình thang cân ABCD có: AD = 2cm, CD = 4cm, AC = 3,5cm thỏa mãn yêu cầu bài toán.
Biện luận: Tam giác ADC luôn dựng được nên hình thang ABCD luôn dựng được. Cung tròn tâm D bán kính 3,5cm cắt Ax tại 1 điểm nên ta dựng được một hình thang thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)

















