a)Xét 2 tam giác vuông ABC và DEC có

góc C chung

=> ABC~DEC(g.g)

b)TÍnh BC

Áp dụng định lí pi-ta-go vào tam giác vuông ABC

\(BC^2=AB^2+AC^2\)hay \(BC^2=3^2+5^2\)\(\Leftrightarrow\)\(BC^2=9+25\Rightarrow BC=\sqrt{9+25}\approx5,9\)

*TÍnh BD

Vì AD là tia fân giác của góc BAC nên ta có

\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{5}\)hay \(\frac{BD}{3}=\frac{DC}{5}\)

Áp dụng tính chất dãy tỉ số bằng nhau

\(\frac{BD+DC}{3+5}=\frac{BC}{8}=\frac{5,9}{8}\)

\(\Rightarrow\)\(\frac{BD}{3}=\frac{5,9}{8}\Rightarrow BD=\frac{3.5,9}{8}=2,2125\)(cm)

xét \(\Delta ABC\) vuông tại A có AH là đường cao

Áp dụng hệ thức lượng tam giác

\(=>AH^2=BH.HC=>HC=\dfrac{AH^2}{BH}=\dfrac{5^2}{4}=6,25cm\)

b, từ ý a=>\(BC=HB+HC=4+6,25=10,25cm\)

\(\)áp dụng hệ thức lượng \(=>AB^2=BH.BC=>AB=\sqrt{4.10,25}=\sqrt{41}cm\)

\(=>\cos\angle\left(ABC\right)=\dfrac{AB}{BC}=\dfrac{\sqrt{41}}{10,25}cm\)

(bài này chỉ tính 1 tỉ só thôi à bn? nếu tính hết thì bảo nhé)

Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

a) Xét \(\Delta ABC\) vuông tại `A`

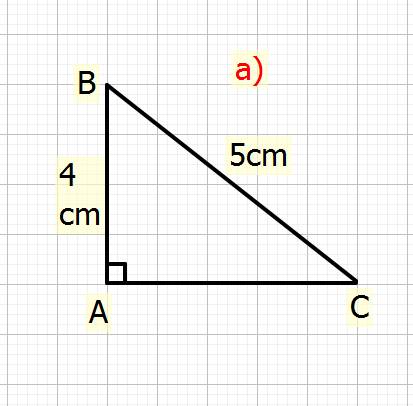
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\) 

Vậy: \(AC=3cm\)

Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)

Vậy: Góc C khoảng \(53^o\)

Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)

\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)

Vậy: Góc B khoảng \(37^o\) 

_

b) Xét \(\Delta ABC\) vuông tại `A`

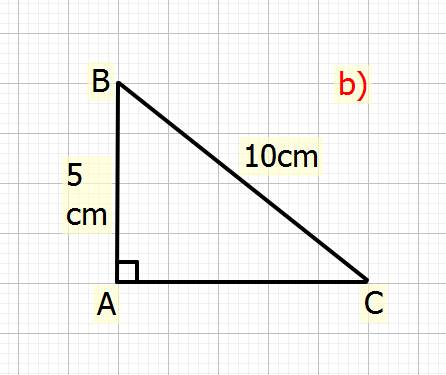
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)

Vậy: \(AC=5\sqrt{3}cm\)

Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)

 \(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)

Vậy: Góc C là \(30^o\)

Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)

Vậy: Góc B là \(60^o\).

Tam giac ABC đồng dạng tam giác HAC (cùng vuông và có chung góc C) 

AB/AC = AH/HC = 20/21 

HC = 21AH/20 = 441 

==> AC = căn(AH^2 + HC^2) =căn(420^2 + 441^2) = 609 

AB/AC = 20/21 
AB = 20/21*609 = 580 

BC = căn(AB^2 + AC^2) = căn(580^2 + 609^2) = 841 

Chu vi tam giác ABC = tổng 3 cạnh 

C = AB + AC + BC = 580 + 609 + 841 = 2030

Xét tg ABC vuông tại A, có:

a. \(BC^2=AB^2+AC^2\left(Pytago\right)\)

\(=>BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\sqrt{8}\right)^2+\left(\sqrt{17}\right)^2}=5\left(cm\right)\)

b. \(BC^2=AB^2+AC^2\left(Pytago\right)\)

\(=>BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{3}{5}\right)^2+\left(\dfrac{4}{5}\right)^2}=1\left(cm\right)\)

a, Xét Tam giác ABC vuôgn tại A

Theo định lí Pi-ta-go, ta có:

 \(AB^2+AC^2=BC^2\)

Hay \(\sqrt{8}+\sqrt{17}=\sqrt{25}=5\left(cm\right)\)

Vậy BC = 5 (cm)

b, Xét tam giác ABC vuôgn tại A

THeo định lí Pi-ta-go, ta có :

\(AB^2+AC^2=BC^2\)

hay \(\left(\dfrac{3}{5}\right)^2+\left(\dfrac{4}{5}\right)^2=\sqrt{\dfrac{9}{25}+\dfrac{16}{25}=1}\)

Vậy BC = 1cm