Cho tam giác ABC : A = 50 độ ; B = 70 độ . Tia phân giác của C cắt canh AB tại M . Tính AMC và BMC

Những câu hỏi liên quan
cho tam giác abc có a =cạnh 50 độ , B = cạnh 65 độ .cm tam giác abc cân
\(\widehat{C}=180^0-50^0-65^0=65^0=\widehat{B}\)
=>ΔABC cân tại A
Đúng 1
Bình luận (0)
cho tam giác abc với góc a=80 độ ; góc b=50 độ
a) tìm cạnh lớn nhất của tam giác abc
b) tam giác abc là tam giác gì ?
a) ta có: góc a + góc b + góc c = 180
hay 80 + 50 + góc c = 180
=> góc c = 180 - 80 - 50 = 50 độ
vì 80 độ > 50 độ => góc a là góc lớn nhất trong tam giác => cạnh lớn nhất là cạnh bc (vì cạnh đối diện với góc lớn hơn là cạnh lớn hơn)
b) \(\Delta ABC\) là tam giác cân vì có 2 góc ở đáy bằng nhau, đều bằng 50 độ
Đúng 1
Bình luận (0)
a, trong tam giác abc có góc a=80 độ,góc b= 50 độ
=>góc c =50 độ
=>góc a là góc lớn nhất
=>cạnh đối diện với góc a là bc
=>bc lớn nhất
b,vì góc b=50độ;góc c=50 độ
=>tam giác abc cân ở a
Đúng 1
Bình luận (0)
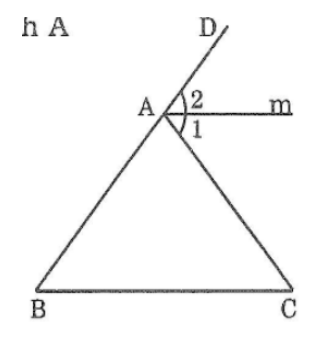
Cho tam giác ABC có <B=50 độ; <C=50 độ. GỌI Am là tia phân giác của góc ngoài đỉnh A của tam giác ABC. Chứng minh: Am//Bc
Trong Δ ABC có ∠(CAD ) là góc ngoài đỉnh A
⇒∠(CAD ) =∠B +∠C =50o+50o=100o
(tính chất góc ngoài tam giác)
∠(A1 ) =∠(A2 ) =1/2 ∠(CAD) =50o (vì tia Am là tia phân giác của ∠(CAD)
Suy ra: ∠(A1) =∠C =50o
⇒ Am // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
cho hai tam giác ABC , DEF có góc A=50 độ , góc E=70 độ , góc F=60 độ , AB=DE , AC=DE . Chứng minh : tam giác ABC=tam giác DEF
\(\widehat{D}=180^0-\widehat{E}-\widehat{F}=50^0=\widehat{A}\\ \left\{{}\begin{matrix}AB=DE\\\widehat{A}=\widehat{D}\\AC=DE\end{matrix}\right.\Rightarrow\Delta ABC=\Delta DEF\left(c.g.c\right)\)
Đúng 2
Bình luận (0)
Cho 2 tam giác ABC, tam giác DEF có góc A = 50 độ , góc E = 70 độ , góc F= 60 độ ,AB=DE,AC=DF. Chứng minh tam giác ABC=tam giác DEF
Xét t/giác DEF có \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\) (tổng 3 góc của 1 t/giác)
=> \(\widehat{D}=180^0-\widehat{E}-\widehat{F}=180^0-70^0-60^0=50^0\)
Xét t/giác ABC và t/giác DEF
có: AB = DE (gt)
AC = DF (gt)
\(\widehat{A}=\widehat{D}=50^0\)
=> t/giác ABC = t/giác DEF (c.g.c)
Cho 2 tam giác ABC, tam giác DEF có góc A = 50 độ , góc E = 70 độ , góc F= 60 độ ,AB=DE,AC=DF. Chứng minh tam giác ABC=tam giác DEF
Ta có tam giác ABC cân tại A -> góc B = Góc C mà góc B = 50 độ -> góc C = 50 độ Xét tam giác ABC có góc A + góc B + góc C= 180 độ ( định lý tổng 3 góc trong tam giác)hay góc A + 50 + 50= 180
Cho tam giác ABC có góc A=80 độ,góc B=50 độ.chứng minh tam giác ABC cân
Xét tam giác ABC, có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(80^o+50^o+\widehat{C}=180^o\)
=> \(\widehat{C}=50^o\)
Ta có:
\(\widehat{B}=50^o\)
\(\widehat{C}=50^o\)
Suy ra: \(\widehat{B}=\widehat{C}\)
=> Tam giác ABC cân tại A.
Góc C bằng :
180o-80o-500=50o
vì Góc C =Góc B nên suy ra Tam giác ABC là tam giác cân
cho tam giác ABC có góc A=50 độ góc C=30 độ. S
o sánh các cạnh của tam giác
Xét Δ ABC
Ta có :
A + B + C = 180º
=> 80º + B = 180º
=> B = 100º
Vậy : C < A < B (30º < 50º < 100º)
Đúng 1
Bình luận (1)
Cho tam giác ABC ,A = 50 độ , B : C = 2:3 . So sánh các cạnh của tam giác ABC
\(\Delta ABC\)CÓ A+B+C=1800
MÀ A=500(GT)
\(\Rightarrow B+C=130^0\)
MÀ \(B\div C=2\div3\)
\(\Rightarrow\frac{B}{2}=\frac{C}{3}\)
ÁP DỤNG TC DÃY TỈ SỐ
=>B=52
C=78
\(\Delta ABC\)CÓ C>B>A
VẬY AB>AC>BC
Đúng 0
Bình luận (0)