xét 2 tam giác vuông ABC và tam giác EDF, ta có: 
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF 
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)

Cho tam giác ABC và tam giác DEF có: AB=DE,BC=EF,AC=DF.

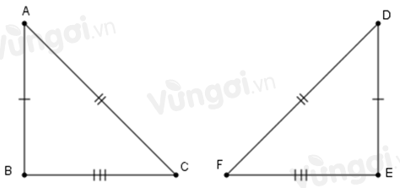
Xét ΔABC và ΔDEF có:

AB=DE(gt)

BC=EF(gt)

AC=DF(gt)

⇒ΔABC=ΔDEF (c.c.c).

Học tốt nhé!

Xét ΔABC vuông tại A và ΔDEF vuông tại D có 

BC=EF(gt)

AC=DF(gt)

Do đó: ΔABC=ΔDEF(cạnh huyền-cạnh góc vuông)

Cách 1:

Xét tam giác $ABC$ và $DEF$ có:

$\widehat{A}=\widehat{D}=90^0$

$BC=EF$

$AC=DF$

$\Rightarrow \triangle ABC=\triangle DEF$ (ch-gcv)

Cách 2:

Vì $BC=EF; AC=DF\Rightarrow BC^2-AC^2=EF^2-DF^2$ hay $BA^2=ED^2$

$\Leftrightarrow BA=ED$ (theo định lý Pitago)

Hai tam giác $ABC$ và $DEF$ có các cạnh $AB=DE, BC=EF, AC=DF$ nên bằng nhau theo TH c.c.c

Tự vẽ hình~

Xét tam giác ABC và tam giác DFE

\(\frac{AB}{EF}=\frac{6}{12}=\frac{1}{2}\)

\(\frac{AC}{FE}=\frac{9}{18}=\frac{1}{2}\)

 \(\frac{BC}{DE}=\frac{12}{24}=\frac{1}{2}\)

\(\Rightarrow\frac{AB}{DF}=\frac{AC}{FE}=\frac{BC}{DE}=\frac{1}{2}\)

=>Tam giác ABC đồng đang với tam giác DFE (c.c.c)

Xét ΔDAF và ΔEBD có

DA=EB

góc DAF=góc EBD(=120 độ)
AF=BD

=>ΔDAF=ΔEBD

=>DF=ED

Xét ΔFCE và ΔEBD có

FC=EB

góc FCE=góc EBD

CE=BD

=>ΔFCE=ΔEBD

=>FE=ED

=>FE=ED=DF

=>ΔDEF đều

\(\widehat{B}=\widehat{E}\)

Xét ΔBDE và ΔAFD có

BE=AD

góc EBD=góc DAF

AF=BD

=>ΔBDE=ΔAFD

=>DE=FD

Xét ΔBDE và ΔCEF có

BE=CF

góc DBE=góc ECF

BD=CE

=>ΔBDE=ΔCEF

=>DE=EF=FD

=>ΔDEF đều

a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có 

AB/DE=AC/DF

Do đó: ΔABC\(\sim\)ΔDEF

b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)