cho hình bs 10 (hai đường thẳng ab song song với nhau và hai đường thẳng c,d song song với nhau ; Dm,Cp,Bq và An tương ứng là các tia phân giác). a) Chứng minh : An // Cp và Dm // Bq. b) Chứng minh : An vuông góc với Bq
Cho hình bs 10 (hai đường thẳng ab song song với nhau và hai đường thẳng c,d song song với nhau ; Dm,Cp,Bq và An tương ứng là các tia phân giác). a) Chứng minh : An // Cp và Dm // Bq. b) Chứng minh : An vuông góc với Bq
cho hình bs 10 (hai đường thẳng a,b song song với nhau và hai đường thẳng c,d song song với nhau ; Dm,Cp,Bq và An tương ứng là các tia phân giác).
a) Chứng minh : An // Cp và Dm // Bq.
b) Chứng minh : An vuông góc với Bq
Cho hình bs 10 (hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).
Chứng minh: An vuông góc với Bq.
Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Cho hình bs 10 (hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).
Chứng minh: An // Cp và Dm // Bq.
Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
Cho hình bs 10 (hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác)
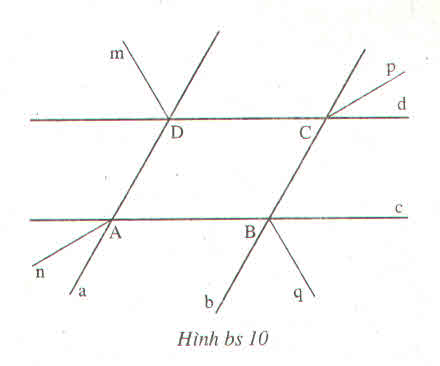
a) Chứng minh : An // Cp và Dm //Bq
b) Chứng minh : An vuông góc với Bq
Cho hình bs 10 (hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác)
a) Chứng minh : An // Cp và Dm //Bq
b) Chứng minh : An vuông góc với Bq
Cho hình chóp tứ giác đều \(A.MNPQ\) (Hình 5)
a) Hãy cho biết đỉnh, cạnh bên, mặt bên, cạnh đáy, mặt đáy, đường cao của hình chóp tứ giác đều đó.
b) Cho biết \(AM = 5\)cm, \(MN = 4\)cm. Tìm độ dài các cạnh \(AN\), \(AP\), \(AQ\), \(NP\), \(PQ\), \(QM\)
- Mặt bên: \(MAB\), \(MAC\), \(MBC\)
- Mặt đáy: \(ABC\)
- Đường cao: \(MO\)
- Độ dài cạnh bên: \(15\)cm
- Độ dài cạnh đáy: \(10\)cm
Cho hình bs 10(hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).
a) Chứng minh: An // Cp và Dm // Bq.
b) Chứng minh: An vuông góc với Bq.
Cho tam giac ABC . Bên ngoài tam giac ABC , dựng các hình vuông ABMN và BCQP. Gọi D, E, G, H lần lượt là trung điểm của AC, BN, MP, BQ. Chứng minh rằng tứ giác DEGH là hình vuông.
\(\left\{{}\begin{matrix}\widehat{ABP}=\widehat{MBC}\left(=\widehat{ABC}+90^0\right)\\BA=BM\\BP=BC\end{matrix}\right.\Rightarrow\Delta BAP=\Delta BMC\left(c.g.c\right)\\ \Rightarrow AP=CM;\widehat{BAP}=\widehat{BMC}\)
Gọi \(\left\{O\right\}=AP\cap CM\)
\(\widehat{AIO}=\widehat{BIM}\left(đđ\right)\\ \Rightarrow\widehat{AOI}=180^0-\left(\widehat{BAP}+\widehat{AIO}\right)=180^0-\left(\widehat{BMC}+\widehat{BIM}\right)=90^0\)
Lại có HD,DE,EG lần lượt là đtb \(\Delta ACD,\Delta ACM,\Delta APM\)
Do đó \(\left\{{}\begin{matrix}HD\text{//}AP;HD=\dfrac{1}{2}AP\left(1\right)\\DE\text{//}CM;DE=\dfrac{1}{2}CM\left(2\right)\\EG\text{//}AP;EG=\dfrac{1}{2}AP\left(3\right)\end{matrix}\right.\)
\(\left(1\right)\left(3\right)\Rightarrow HD\text{//}EG;HD=EG\\ \Rightarrow DEGH\text{ là hbh}\\ \text{Mà }AP=CM\Rightarrow HD=HE\\ \Rightarrow DEGH\text{ là hình thoi}\)
Mặt khác: \(DE\text{//}CM;AP\bot CM\Rightarrow AP\bot DE\)
Mà \(HD\text{//}AP\Rightarrow DE\text{//}HD\)
Vậy DEGH là hình vuông
