Bài 1:

Áp dụng HTL trong tam giác vuông:

$AB^2=BH.BC$

$\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{10}=3,6$ (cm)

$CH=BC-BH=10-3,6=6,4$ (cm)

Tiếp tục áp dụng HTL: 

$AH^2=BH.CH=3,6.6,4$

$\Rightarrow AH=4,8$ (cm)

$AC^2=CH.BC=6,4.10=64$

$\Rightarrow AC=8$ (cm)

Bài 2:

Áp dụng định lý Pitago:

$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+1^2}=2$ (cm)

$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{\sqrt{3}.1}{2}=\frac{\sqrt{3}}{2}$ (cm)

$BH=\sqrt{AB^2-AH^2}=\sqrt{3-\frac{3}{4}}=\frac{3}{2}$ (cm)

$CH=BC-BH=2-\frac{3}{2}=\frac{1}{2}$ (cm)

3. 

$BC=BH+CH=16a+9a=25a$

Áp dụng HTL trong tam giác vuông:

$AH^2=BH.CH=16a.9a=(12a)^2$

$\Rightarrow AH=12a$ (do $a>0$)

$AB=\sqrt{BH^2+AH^2}=\sqrt{(16a)^2+(12a)^2}=20a$

$AC=\sqrt{CH^2+AH^2}=\sqrt{(9a)^2+(12a)^2}=15a$

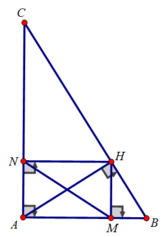
a) Xét tam giác ABC vuông tại A, đường cao AH có:

B C 2 = A B 2 + A C 2 = 25 ⇒ BC = 5(cm)

AB2 = BH.BC ⇒ BH = AB2/BC = 9/5 = 1,8(cm)

BH + CH = BC⇒ CH = BC - BH = 5 - 1,8 = 3,2 (cm)

A H 2 = BH.CH ⇒ AH = B H . C H = 1 , 8 . 3 , 2 = 2,4 (cm)

Xét tứ giác AMHN có:

∠(MAN) = ∠(ANH) = ∠(AMH) = 90 0

⇒ Tứ giác AMHN là hình chữ nhật

⇒ MN = AH = 2,4 (cm)

a.  - Áp dụng hệ thức về cạnh và đường cao trong Δ vuông vào ΔABC vuông tại A ta có :

            \(AH=\sqrt{CH.BH}=\sqrt{2.4}=2\sqrt{2}\)     ( Đ.lý 2 )

    - Áp dụng đ.lý Pytago vào \(\Delta AHB\perp H\) ta có :

         \(AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{2}\right)^2+4^2}=2\sqrt{6}\)

   - \(BC=2+4=6\)

   - Theo đ.lý Pytago :

       \(AC=\sqrt{BC^2-AB^2}=\sqrt{6^2-\left(2\sqrt{6}\right)^2}=2\sqrt{3}\)

b.  - Áp dụng hệ thức...trong Δ vuông ABC ta có :

          + \(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=24\)   ( Đ.lý 1 )

        \(\Rightarrow CH=BC-BH=24-6=18\)

          + \(AH=\sqrt{BH.CH}=\sqrt{6.18}=6\sqrt{3}\)   ( Đ.'ý 2 )

   - Theo đ.lý Pytago ta có :

      \(AC=\sqrt{BC^2-AB^2}=\sqrt{24^2-12^2}=12\sqrt{3}\)

a, BC = BH+HC 

*\(AB=\sqrt{BH.BC}=\sqrt{4.8}=\sqrt{32}\)

*\(AC=\sqrt{HC.BC}=\sqrt{2.8}=4\)

*\(AH=\sqrt{BH.HC}=\sqrt{4.2}=\sqrt{8}\)

b,Theo định lý pytago ta có:

\(AH=\sqrt{AB^2-BH^2}=\sqrt{12^2-6^2}=6\sqrt{3}\)

*\(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=2\)

*\(CH=BC-BH=24-6=18\)

\(AC=\sqrt{HC.BC}=\sqrt{18.24}=12\sqrt{3}\)

a, BC = BH+HC 

*\(AB=\sqrt{BH.BC}=\sqrt{4.8}=\sqrt{32}\)

*\(AC=\sqrt{HC.BC}=\sqrt{2.8}=4\)

*\(AH=\sqrt{BH.HC}=\sqrt{4.2}=\sqrt{8}\)

b,Theo định lý pytago ta có:

\(AH=\sqrt{AB^2-BH^2}=\sqrt{12^2-6^2}=6\sqrt{3}\)

*\(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=2\)

*\(CH=BC-BH=24-6=18\)

\(AC=\sqrt{HC.BC}=\sqrt{18.24}=12\sqrt{3}\)

Bạn chỉ cần áp dụng hệ thức lượng là đc rồi o0o

Cho tam giác ABC vuông tại A , đường cao AH . Chứng minh rằng 1/AH^2=1/AB^2+1/ac^2

a: AH=căn 13^2-5^2=12cm

CH=12^2/5=28,8cm

BC=28,8+5=33,8cm

AC=căn 28,8*33,8=31,2cm

b: AH=căn 3*4=2căn 3(cm)

AB=căn 3*7=căn 21(cm)

AC=căn 4*7=2căn 7(cm)

c: CH=4^2/3=16/3cm

AB=căn 4^2+3^2=5cm

AC=căn 16/3*25/3=20/3(cm)

a) Xét tam giác ABH vuông tại H, ta có:
AB² = AH² + HB² (ĐL Py-ta-go)
AB² = 15²  + 25²
AB² = 225 + 625
AB² = 850
AB  = \(\sqrt{850}\)(cm)

Xét tam giác ABC vuông tại A, có đường cao AH:
=> BA² = BH.BC
     850 = 25.BC
     BC  = 850:25
     BC  = 34

Xét tam giác ABC vuông tại A, ta có:
BC² = AB² + AC²
34²  = 850 + AC²
1156 - 850 = AC²
AC² = 306
AC = \(\sqrt{306}\)(cm)

Ta có BC = BH + HC
         34 = 25 + HC
         HC = 34 - 25
         HC = 9

b) Xét tam giác ABH vuông tại H, ta có:
AB² = AH² + HB² (ĐL Py-ta-go)
12² = AH² + 6²
144 = AH² + 36
AH² = 144 - 36
AH² = 108
AH = \(\sqrt{108}\)(cm)

Xét tam giác ABC vuông tại A, có đường cao AH:
=> BA² = BH.BC
     12² = 6.BC
     144 = 6.BC
     BC = 144:6
     BC = 24 (cm)

Ta có BC = BH + HC
         24 = 6 + HC
         HC = 24 - 6
         HC = 18

Xét tam giác ABC vuông tại A, ta có:
BC² = AB² + AC² (ĐL Py-ta-go)
24² = 12² + AC²
AC² = 24² - 12²
AC² = 576 - 144
AC² = 432
AC = \(\sqrt{432}\)(cm)

AH=căn 3*4=2căn 3(cm)

AB=căn 3*7=căn 21(cm)

AC=căn 4*7=căn 28(cm)

sin B=AC/BC=căn 28/7=0,7559

sin C=AB/BC=căn 21/7=0,6547

a, AB = 7,5cm, AC = 10cm, BC = 12,5cm, HC = 8cm

b, AH = 3 3 cm;  P A B C = 18 + 6 3 c m ;  P A B H = 9 + 3 3 c m ;  P A C H = 9 + 9 3 c m

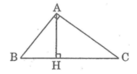
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: A H 2 = B H . C H

⇒ CH =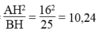 

BC = BH + CH = 25 + 10,24 = 35,24

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

A B 2 = B H . B C ⇒ AB = 

≈ 29,68

A C 2 = H C . B C

⇒ AC =  ≈ 18,99