Cho tam giác ABC vuông tại A có AB = 12 cm ; AC = 16 cm vẽ AH là đường cao, AM là đường trung tuyến của tam giác ABC
a) Tính BH ; HC ; AH
b) Tính diện tích tam giác HMA .
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Cho tam giác ABC vuông tại A, có BC = a, AC = b, AB = c. Giải tam giác ABC, biết:
a, a = 15 cm, b = 10 cm
b, b = 12 cm, c = 7 cm
Cho tam giác ABC vuông tại A có BC = 15 cm, AB = 12 cm. Tính AC, B ^
A. A C = 8 c m ; B ^ ≈ 36 ° 52 '
B. A C = 9 c m ; B ^ ≈ 36 ° 52 '
C. A C = 9 c m ; B ^ ≈ 37 ° 52 '
D. A C = 9 c m ; B ^ ≈ 36 ° 55 '
bài 3;cho tam giác abc vuông tại a biết ab=2cm tính bc
bài 4;cho tam giác abc vuông tại a biết bc=2cm.tính ab,ac
bài 5.cho tam giác abc vuông tại a
a)tính ab biết bc=10cm,ac=8cm.b)tính ac biết bc=12 cm,ab=10cm
Cho tam giác ABC vuông tại A có BC = 15 cm, AB = 12 cm. Tính AC, góc B
A. A C = 8 c m ; B ^ ≈ 36 ° 52 '
B. A C = 9 c m ; B ^ ≈ 36 ° 52 '
C. A C = 9 c m ; B ^ ≈ 37 ° 52 '
D. A C = 9 c m ; B ^ ≈ 36 ° 55 '
Cho tam giác ABC vuông tại A có AB = 9 cm, AC = 12 cm. Gọi I là tâm đường tròn nội tiếp tam giác ABC, G là trọng tâm của tam giác ABC. Tính độ dài IG
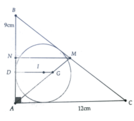
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm
Cho tam giác ABC có AB = 12 cm AH vuông góc BC H thuộc BC BH = 7,2 cm Tính ah biết BH = 12 cm
a) tính ahb) biết ch= 12.8cm tính acc) tam giác abc có phải là tam giác vuông không tại saoa. ta có : tam giác AHB vuông tại H nên
\(AH^2=AB^2-BH^2=12^2-7,2^2=9,6^2\) Vậy AH =9,6cm
b. Ta có : ABC phải tam giác vuông vì \(AB^2=BH.BC\)
cho tam giác ABC vuông tại A có BC =12 cm . Tính chiều dài hai cạnh góc vuông biết AB 2/3 AC
Ta có \(\Delta ABC\) vuông tại A nên:
\(BC^2=AB^2+AC^2\)
Mà: \(AB=\dfrac{2}{3}AC\)
\(\Rightarrow BC^2=\left(\dfrac{2}{3}AC\right)^2+AC^2\)
\(\Rightarrow12^2=\left(\dfrac{2}{3}AC\right)^2+AC\)
\(\Rightarrow144=\dfrac{4}{9}AC^2+AC^2\)
\(\Rightarrow144=\dfrac{13}{9}AC^2\)
\(\Rightarrow AC^2=\dfrac{144}{\dfrac{13}{9}}\approx100\)
\(\Rightarrow AC\approx\sqrt{100}\approx10\left(cm\right)\)
Ta có \(AC=10cm\Rightarrow AB=\dfrac{2}{3}AC=\dfrac{2}{3}\cdot10\approx6,6\left(cm\right)\)
Vậy: ....
Cho tam giác ABC vuông tại A ,AB bằng 9 cm ,AC bằng 12 cm .Kẻ AH vuông góc với BC tại H
a/Chứng minh tam giác abh đồng dạng tam giác ABC và AB mũ 2 = Hb . BC
b/tính BC, ah
c/tia phân giác góc ACB cắt ah tại I và cắt AB tại D Chứng minh CB.CI=CA.CDCD
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
b: BC=căn 9^2+12^2=15cm
AH=9*12/15=7,2cm
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=18^2+20^2=724\)
hay \(BC=2\sqrt{181}cm\)
Vậy: \(BC=2\sqrt{181}cm\)