Giả sử phương trình bậc hai a x 2 + bx + c = 0 có hai nghiệm thuộc [0; 3]. Tìm giá trị lớn nhất của biểu thức: Q = 18 a 2 - 9 a b + b 2 9 a 2 - 3 a b + a c
A. 5
B. 4
C. 2
D. 3
Xét hai câu sau:
P: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\)”.
a) Hãy phát biểu mệnh đề \(P \Rightarrow Q\).
b) Hãy phát biểu mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(P \Rightarrow Q\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\).”
Mệnh đề \(Q \Rightarrow P\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\) thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.”
Giả sử x 1 , x 2 là hai nghiệm của phương trình bậc hai a x 2 + bx + c = 0 có ∆ ’ = 0. Điều nào sau đây là đúng?
A . x 1 = x 2 = b 2 a B . x 1 = x 2 = - b ' a C . x 1 = x 2 = - b a D . x 1 = x 2 = - b ' 2 a
Giả sử x 1 , x 2 là hai nghiệm của phương trình bậc hai a x 2 + bx + c = 0 có ∆’ = 0
Do đó, phương trình có nghiệm kép 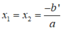
Chọn B
Chứng minh rằng: “Nếu phương trình bậc hai : ax2 + bx + c = 0 vô nghiệm thì a và c cùng dấu”. Một học sinh đã làm như sau:
Bước 1: Giả sử phương trình vô nghiệm và a, c cùng dấu.
Bước 2: Với điều kiện a, c trái dấu ta có a.c > 0 suy ra Δ = b2 - 4ac > 0.
Bước 3: Nên phương trình có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm.
Bước 4: Vậy phương trình vô nghiệm thì a, c phải cùng dấu.
Lập luận trên sai từ bước nào?
A. Bước 1
B. Bước 2
C. Bước 3
D. Bước 4.
Đáp án: A
Bước 1 sai vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.
Câu 1 :Giả sử phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm thuộc [0;3]. Tìm GTLN và GTNN của biểu thức:
Q=\(\frac{18a^2-9ab+b^2}{9a^2-3ab+ac}\)
Câu 2 Giả sử phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm > 1 Chứng minh rằng
\(\frac{^{x^2-a-2b}}{b-a+1}\text{≥}\frac{2\sqrt{b}}{1+\sqrt{b}}\)
GIÚP MÌNH VỚI
Câu 2: Theo định lý Vi-et ta có \(\hept{\begin{cases}x_1+x_2=-a\\x_1x_2=b\end{cases}}\)Bất Đẳng Thức cần chứng minh có dạng
\(\frac{x_1}{1+x_1}+\frac{x_2}{1+x_2}\ge\frac{2\sqrt{x_1x_2}}{1+\sqrt{x_1x_2}}\)Hay \(\frac{x_1}{1+x_2}+1+\frac{x_2}{1+x_1}+1\ge\frac{2\sqrt{x_1x_2}}{1+\sqrt{x_1x_2}}+2\)
\(\left(x_1+x_2+1\right)\left(\frac{1}{1+x_1}+\frac{1}{1+x_2}\right)\ge\frac{2\left(1+2\sqrt{x_1x_2}\right)}{1+\sqrt{x_1x_2}}\)Theo Bất Đẳng Thức Cosi ta có
\(x_1+x_2+1\ge2\sqrt{x_1x_2}+1\)Để chứng minh (*) ta quy về chứng minh
\(\frac{1}{1+x_1}+\frac{1}{1+x_2}\ge\frac{2}{1+\sqrt{x_1x_2}}\)với \(x_1;x_2>1\). Quy đồng rồi rút gọn Bất Đẳng Thức trên tương đương với
\(\left(\sqrt{x_1x_2}-1\right)\left(\sqrt{x_1}-\sqrt{x_2}\right)^2\ge0\)(Điều này hiển nhiên đúng)
Dấu "=" xảy ra khi và chỉ khi \(x_1=x_2\Leftrightarrow a^2=4b\)
Bạn ơi thế a^2 - 4b ở vế trái bạn vứt đi đâu r ????
Giả sử phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm \(x_1,x_2\) thỏa mãn \(x_1^2+x_2^2=2x_1x_2\). Chứng minh rằng biệt thức \(\Delta\) của phương trình không phụ thuộc vào các hệ số a, b,c
Theo Vi et ta có: \(\hept{\begin{cases}x_1+x_2=\frac{-b}{a}\\x_1x_2=\frac{c}{a}\end{cases}}\)
Theo giả thuyết thì:
\(x_1^2+x_2^2=2x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\)
\(\Leftrightarrow\frac{b^2}{a^2}-\frac{4c}{a}=0\)
\(\Leftrightarrow b^2-4ac=0\)
Vậy ta có ĐPCM
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a x 2 + b x + c = 0 ( a ≠ 0 )
Nêu điều kiện để phương trình a x 2 + b x + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954 x 2 + 21 x – 1975 = 0
Nêu điều kiện để phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005 x 2 + 104 x – 1901 = 0
Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
ax2 + bx + c = 0 (a ≠ 0)
Nêu điều kiện để phương trình ax2 + bx + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954x2 + 21x – 1975 = 0
Nêu điều kiện để phương trình ax2 + bx + c = 0 (a ≠ 0) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005x2 + 104x – 1901 = 0
xét phương trình bậc hai ax²+bx+c=0 có hai nghiệm thuộc [0, 2]. tìm giá trị lớn nhất của biểu thức P=(8a²-6ab+b²)/(4a²-2ab+ac)
Cho phuong trình bậc hai ax2 + bx+ c =0 có hai nghiệm x1,x2 deu khác 0 . Phương trình bậc hai nhận 2x1 và 2x2 làm nghiệm là:
x1+x2=-b/a; x1x2=c/a
=>2x1+2x2=-2b/a; 4x1x2=4c/a
=>PT cần tìm là x^2+2b/a*x+4c/a=0