Cho ba vectơ: a → = (2; -5; 3), b → = (0; 2; -1), c → = (1; 7; 2) Tính tọa độ của vectơ d → = 4 a → - 1/3 b → + 3 c →

Những câu hỏi liên quan
Trong không gian Oxyz, cho ba vectơ
a
→
4
;
3
;
−
2
,
b
→
6
;
5
;
1...
Đọc tiếp
Trong không gian Oxyz, cho ba vectơ a → = 4 ; 3 ; − 2 , b → = 6 ; 5 ; 1 , c → = x ; 2 x ; 3 x + 2 . Để ba vectơ a → , b → , c → đồng phẳng thì giá trị của x là:
A. − 4 13
B. 13 4
C. 4 13
D. − 13 4
Đáp án C
Em có: a → , b → = 13 ; − 16 ; 2
Ba vectơ a → , b → , c → đồng phẳng thì a → , b → . c → = 0

Đúng 0
Bình luận (0)
Cho ba vectơ: a→ = (2; -5; 3), b→ = (0; 2; -1), c→ = (1; 7; 2)
Tính tọa độ của vectơ e→ = a→ - 4b→ - 2c→
Ta có: -4b→ = (0; -8; 4)
-2c→ = (-2; -14; -4)
Vậy e→ = a→ - 4b→ - 2c→ = (0; -27; 3)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi D sao cho vectơ BD = 2/3 vectơ BC. i là trung điểm AD. Gọi M là điểm thoả : vectơ AM = x vectơ AC ( x thuộc R )
a) Tính vectơ BM theo vectơ BA và vectơ BC
b) Tính x để ba điểm B, I, M thẳng hàng
tam giác ABC từ A ,B,C dựng vectơ AA'= vectơ BB' = vectơ CC'
chứng minh rằng1. vectơ BB' + vectơ CC'+ vectơ BA' + vectơ CA' = vectơ BA' + vectơ CA'
2. AA'+BB'+CC'=BA'+CB'+AC'
Cho tam giác ABC. Gọi D là điểm định bởi vectơ BD=2/3 vectơ BC, I là trung điểm của AD. Gọi M là điểm thõa vectơ AM=x vectơ AC (x thuộc R)
a) Tính vectơ BI theo vectơ BA và vectơ BC.
b) Tính vectơ BM theo vectơ BA và vectơ BC.
c) Tính x để 3 điểm B, I, M thẳng hàng
Trong không gian Oxyz, cho ba vectơ
a
→
(
2
;
-
5
;
3
)
,
b
→
(
0
;
2
;
-
1
)
,
c
→
1
;
7
;
2
. Tọa độ vectơ...
Đọc tiếp
Trong không gian Oxyz, cho ba vectơ a → = ( 2 ; - 5 ; 3 ) , b → = ( 0 ; 2 ; - 1 ) , c → = 1 ; 7 ; 2 . Tọa độ vectơ x → = 4 a → - 1 3 b → + 3 c → là:
![]()
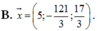
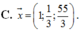
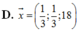
Trong không gian Oxyz, cho ba vectơ
a
→
2
;
-
5
;
3
,
b
→
0
;
2
;
-
1
,
c
→
1...
Đọc tiếp
Trong không gian Oxyz, cho ba vectơ a → = 2 ; - 5 ; 3 , b → = 0 ; 2 ; - 1 , c → = 1 ; 7 ; 2 . Tọa độ vectơ x → = 4 a → - 1 3 b → + 3 c → là:
A. x → = 11 ; 5 3 ; 53 3
B. x → = 5 ; - 121 3 ; 17 3 .
C. x → = 11 ; 1 3 ; 55 3
D. x → = 1 3 ; 1 3 ; 18
Cho ΔABC đều, cạnh a
Tính độ dài các vectơ
vectơ u = vectơ AB + vectơ AC
vectơ v = vectơ CA + vectơ BA
vectơ w = vectơ AB - vectơ AC
vectơ t = vectơ AB - vectơ CA
vectơ a = vectơ AB - vectơ BC
Gọi M là trung điểm của BC
Vì ΔABC đều
mà M là trug điểm của bC
nên MA vuông góc với BC
BM=CM=a/2
\(AM=\sqrt{a^2-\left(\dfrac{1}{2}a\right)^2}=\dfrac{a\sqrt{3}}{2}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{BA}\right|=2\cdot AM=2\cdot\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=a\)
\(\left|\overrightarrow{AB}-\overrightarrow{CA}\right|=\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{3}\)
vecto AB-vecto BC
=vecto AB+vecto CB
=>|vecto AB+vecto CB|=|vecto BA+vecto BC|=|2vecto BN|(Với N là trung điểm của AC)
=2xBN=a căn 3
Đúng 0
Bình luận (0)
Trong không gian cho ba vectơ a , b và c đều khác vectơ 0 . Khi nào ba véc tơ đó đồng phẳng?
Ba vectơ a → ; b → v à c → đồng phẳng nếu thỏa mãn một trong hai điều kiện sau:
- Giá của 3 vector đều cùng song song với mặt phẳng (P).
- 1 trong 3 vec tơ biểu diễn được qua hai vec tơ còn lại,
tức là tồn tại cặp số (m; n) duy nhất thỏa mãn 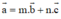
Đúng 0
Bình luận (0)










