a) Phương trình đường tròn là: \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 81\)

b) Bán kính đường tròn là: \(R = IM = \sqrt {{{\left( {4 - 5} \right)}^2} + {{\left( { - 1 + 2} \right)}^2}}  = \sqrt 2 \)

Phương trình đường tròn là: \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} = 2\)

c) Bán kính đường tròn là: \(R = \frac{{\left| {5.1 - 12.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = \frac{{16}}{{13}}\)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {\left( {\frac{{16}}{{13}}} \right)^2}\)

d) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( {1;1} \right)\)

Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( { - 4 - 1} \right)}^2}}  = \sqrt {29} \)

Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 29\)

e) Giả sử  tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)

Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {1 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2}\\{\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {0 - a} \right)^2} + {\left( {4 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\)  b

Vậy \(I\left( {2;3} \right)\) và \(R = IA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}}  = \sqrt 5 \)

Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 5\)

a) HS tự vẽ hình.

b) Hai đường tròn trên có đi qua O và I. Chúng có cắt nhau.

a) HS tự vẽ hình.

b) Hai đường tròn trên có đi qua O và I. Chúng có cắt nhau.

gọi a là đường kính đường tròn tâm I => đường kính đường tròn tâm O là 2a

S_{tâm I} = d x 3,14 = a x 3,14 = 3,14a

S_{tâm O}= d x 3,14 = 2a x 3,14 = 6,28a

S_{tâm O} / S_{tâm I} = 6,28a / 3,14a = 2 

Vậy S_{tâm O} gấp 2 lần S_{tâm I}

Gấp 4 lần

                                       Giả sử đường kính của hình tròn tâm o là  4 thì đường kính của hình tròn tâm i là 4:2=2

                                                                                  Bán kính của hình tròn tâm o là:

                                                                                                      4:2=2

                                                                                  Bán kính của hình tròn tâm i là:

                                                                                                      2:2=1

                                                                                 Diện tích của hình tròn tâm o là:

                                                                                              2x2x3,14=12,56

                                                                                 Diện tích của hình tròn tâm i là:

                                                                                             1x1x3,14=3,14

                                                        Diện tích hình tròn tâm o gấp số lần diện tích hình tròn tâm i là:

                                                                                             12,56:3,14=4 (lần)

                                                                                                  Đáp số:4 lần

Đáp án là B

Do AB là đường kính đường tròn (O); C nằm trên đường tròn nên ΔCAB vuông tại C

Mặt khác tâm đường tròn nội tiếp là giao điểm 3 đường phân giác trong

⇒ I thuộc cung chứa góc 45 0  dựng trên đoạn AB.

Ta có: đường tròn (C₁) : 

Vậy (1) đúng

Đường tròn ( C₂): 

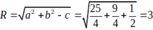
Vậy (2) đúng.

Chọn C.