Cho 2 số thực a,b thay đổi thỏa mãn đk : a + b >= 0; 1>a>0
Tính GTNN của A=\(\frac{8a^2+b}{4a}\)+ b\(^2\)
Cho hai số thực x,y khác 0 thay đổi và thỏa mãn đk \(\left(x+y\right)xy=x^2+y^2-xy\). GTLN của bthuc \(M=\dfrac{1}{x^3}+\dfrac{1}{y^3}\)
a,b,c là các số thực thay đổi và thỏa mãn abc=-2, a+b+c=0 tìm GTNN của bt F=(ab+bc+ac-a^2-b^2-c^2)/(a^3+b^3+c^3)
\(a+b+c=0\) nên trong 3 số a;b;c phải có ít nhất 1 số dương
Do vai trò của 3 biến như nhau, ko mất tính tổng quát, giả sử \(c>0\)
\(a+b+c=0\Rightarrow\left(a+b+c\right)^2=0\)
\(\Rightarrow a^2+b^2+c^2=-2\left(ab+bc+ca\right)\)
\(a^3+b^3+c^3=a^3+b^3+3ab\left(a+b\right)+c^3-3ab\left(a+b\right)\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)=\left(-c\right)^3+c^3-3ab\left(-c\right)=3abc=-6\)
\(\Rightarrow F=\dfrac{ab+bc+ca-\left(a^2+b^2+c^2\right)}{-6}=\dfrac{3\left(ab+bc+ca\right)}{-6}=\dfrac{ab+bc+ca}{-2}\)
\(=\dfrac{-\dfrac{2}{c}+c\left(a+b\right)}{-2}=\dfrac{-\dfrac{2}{c}+c\left(-c\right)}{-2}=\dfrac{c^2}{2}+\dfrac{1}{c}=\dfrac{c^2}{2}+\dfrac{1}{2c}+\dfrac{1}{2c}\ge3\sqrt[3]{\dfrac{c^2}{8c^2}}=\dfrac{3}{2}\)
\(F_{min}=\dfrac{3}{2}\) khi \(\left(a;b;c\right)=\left(-2;1;1\right)\) và các hoán vị
Cho hai số thực a,b thay đổi thỏa mãn 4a+b-1-(1/2)3a+b-2+5a+3b-4=0. Tìm GTNN của biểu thức P=a2+2ab+b2
\(4^{a+b-1}-\left(\frac{1}{2}\right)^{3a+b-2}+5a+3b-4=0\)
\(\Leftrightarrow2^{2a+2b-2}-2^{-3a-b+2}+5a+3b-4=0\)
\(\Leftrightarrow2^{2a+2b-2}+2b+2b-2=2^{-3a-b+2}-3a-b+2\)(1)
Xét hàm \(f\left(t\right)=2^t+t\)
\(f'\left(t\right)=2^t.ln\left(2\right)+1>0,\forall t\inℝ\)
suy ra \(f\left(t\right)\)đồng biến trên \(ℝ\).
(1) suy ra \(2a+2b-2=-3a-b+2\Leftrightarrow b=\frac{4-5a}{3}\)
\(P=a^2+2ab+b^2=\left(a+b\right)^2=\left(a+\frac{4-5a}{3}\right)^2\ge0\)
Dấu \(=\)khi \(a=2\).
Vậy \(minP=0\)khi \(a=2,b=-2\)
Xét các số thực a,b,c thay đổi thỏa mãn \(0\le a\le1\le b\le2\le c\) và \(a+b+c=5\) . Tìm giá trị lớn nhất của biểu thức \(A=a^2+b^2+c^2\) .
Do \(\left\{{}\begin{matrix}a\ge0\\b\ge1\\a+b+c=5\end{matrix}\right.\) \(\Rightarrow c\le4\)
\(\Rightarrow2\le c\le4\Rightarrow\left(c-2\right)\left(c-4\right)\le0\Rightarrow c^2\le6c-8\)
\(0\le a\le1< 6\Rightarrow a\left(a-6\right)\le0\Rightarrow a^2\le6a\)
\(1\le b\le2< 5\Rightarrow\left(b-1\right)\left(b-5\right)\le0\Rightarrow b^2\le6b-5\)
Cộng vế:
\(a^2+b^2+c^2\le6\left(a+b+c\right)-13=17\)
\(A_{max}=17\) khi \(\left(a;b;c\right)=\left(0;1;4\right)\)
Cho các số thực a;b;c;d thay đổi, luôn thỏa mãn a - 1 2 + b - 2 2 = 1 và 4 c - 3 d - 23 = 0 . Giá trị nhỏ nhất của biểu thức P : a - c 2 + b - d 2 là:
A. P m i n = 28
B. P m i n = 3
C. P m i n = 4
D. P m i n = 16
Gọi M a ; b ; N c ; d
Khi đó ta có M thuộc đường tròn x - 1 2 + y - 2 2 = 1 C và N thuộc đường thẳng
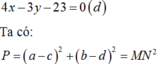
Đường tròn (C) có tâm I 1 ; 2 , bán kính R = 1
Ta có

Khi đó

Chọn D.
Cho a,b,c là 3 số dương cho trước còn x,y,z là ba số dương thay đổi, luôn luôn thỏa mãn ĐK : \(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}=1\)
Đề bài mik chép thiếu : Hãy tìm GTLN của S = x + y + z
Cho các số thực a, b, c, d thay đổi luôn thỏa mãn a − 3 2 + b − 6 2 = 1 v à 4 c + 3 d − 5 = 0 . Tính giá trị nhỏ nhất của T = c − a 2 + d − b 2
A. 16
B. 18
C. 9
D. 15
Trong không gian Oxyz, cho ba điểm A (a;0;0) B (1;b;0) C (1;0;c) với a, b, c là các số thực thay đổi thỏa mãn H (3;2;1) là trực tâm của tam giác ABC. Tính S = a + b + c
\(\overrightarrow{AB}=\left(1-a;b;0\right);\overrightarrow{AC}=\left(1-a;0;c\right);\overrightarrow{HC}=\left(-2;-2;c-1\right);\overrightarrow{HB}=\left(-2;b-2;-1\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}.\overrightarrow{HC}=0\\\overrightarrow{AC}.\overrightarrow{HB}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-2\left(1-a\right)-2b=0\\-2\left(1-a\right)-c=0\end{matrix}\right.\) \(\Rightarrow c=2b=2\left(a-1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(bc;c\left(a-1\right);b\left(a-1\right)\right)=\left(2\left(a-1\right)^2;2\left(a-1\right)^2;\left(a-1\right)^2\right)=\left(a-1\right)^2.\left(2;2;1\right)\)
A;B;C;H đồng phẳng
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right].\overrightarrow{HB}=0\Rightarrow2.\left(-2\right)+2.\left(-2\right)+1.\left(c-1\right)=0\)
\(\Rightarrow c=9\Rightarrow b=\dfrac{9}{2}\Rightarrow a=\dfrac{11}{2}\)
Cho các số thực không âm a, b, c thay đổi thỏa mãn \(a^2+b^2+c^2=1\). Tìm GTLN và GTNN của biểu thức \(Q=\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\)